Задача 49578 ...
Условие
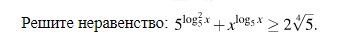
Решение
По свойству степени a^(n^2)=a^(n*n)=(a^(n))^(n)
[m]5^{log^2_{5}x}=(5^{log_{5}x})^{log_{5}x}=x^{log_{5}x}[/m]
Поэтому
[m]x^{log_{5}x}+x^{log_{5}x} ≥ 2\sqrt[4]{5}[/m]
[m]2\cdot x^{log_{5}x} ≥ 2\sqrt[4]{5}[/m]
[m]x^{log_{5}x} ≥ \sqrt[4]{5}[/m]
Логарифмируем по основанию [b]5[/b]
Логарифмическая функция с основанием 5 возрастающая, знак неравенства сохраняется:
[m]log_{5}x^{log_{5}x} ≥log_{5}5^{\frac{1}{4}}[/m]
свойства логарифма степени:
[m]log_{5}x\cdot log_{5}x ≥\frac{1}{4}[/m]
[m]log^2_{5}x-\frac{1}{4} ≥ 0[/m]
[m](log_{5}x-\frac{1}{2})(log_{5}x+\frac{1}{2}) ≥ 0[/m]
[m]-\frac{1}{2} ≤ log_{5}x ≤ \frac{1}{2}[/m]
[m]-\frac{1}{2} log_{5}5≤ log_{5}x ≤ \frac{1}{2} log_{5}5[/m]
[m] log_{5}5^{-\frac{1}{2}} ≤ log_{5}x ≤ log_{5}5^{ \frac{1}{2}}[/m]
[m] 5^{-\frac{1}{2}} ≤x ≤5^{ \frac{1}{2}}[/m]
О т в е т. [1/sqrt(5); sqrt(5)]