Задача 49551 При каких значениях a уравнение...

vk386426418

7 мая 2020 г. в 14:12

При каких значениях a уравнение |x–2|+|x|–ax=2(a–1) имеет ровно один корень?

sova

7 мая 2020 г. в 22:29

|x–2|+x=ax+2a–2

|x–2|+x+2=a·(x+2)

[m]\frac{|x-2|+|x|+2}{x+2}=a[/m]

Найдем при каких значениях параметра а прямая y=a

имеет с графиком [m]y=\frac{|x-2|+|x|+2}{x+2}[/m]

ровно две общие точки.

x=0; x=2 – нули подмодульных выражений.

Они разбивают числовую прямую на три промежутка.

Раскрываем знак модуля на каждом промежутке

(– ∞ ;0]
[m]y=\frac{-x+2-x+2}{x+2}[/m]

[m]y=\frac{-2x+4}{x+2}[/m]

[m]y=\frac{-2x-4+8}{x+2}[/m]

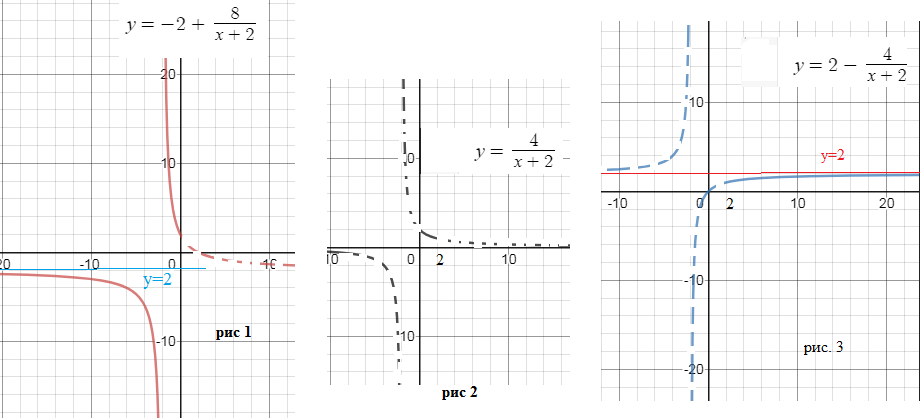
[m]y=-2+\frac{8}{x+2}[/m] – гипербола

на (– ∞ ;0] ( рис. 1)

(0;2]
[m]y=\frac{-x+2+x+2}{x+2}[/m]

[m]y=\frac{4}{x+2}[/m] – гипербола
на (0 ;2] ( рис. 2)

(2;+ ∞ )
[m]y=\frac{x-2+x+2}{x+2}[/m]

[m]y=\frac{2x}{x+2}[/m]

[m]y=\frac{2x+4-4}{x+2}[/m]

[m]y=2-\frac{4}{x+2}[/m] – гипербола

на (2 ;+ ∞ ] ( рис. 3)

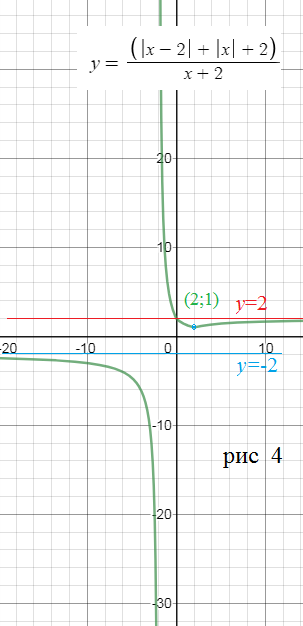
график функции [m]y=\frac{|x-2|+|x|+2}{x+2}[/m] cм
рис 4

О т в е т. (– ∞ ;–2)U{1}U[2;+ ∞ )