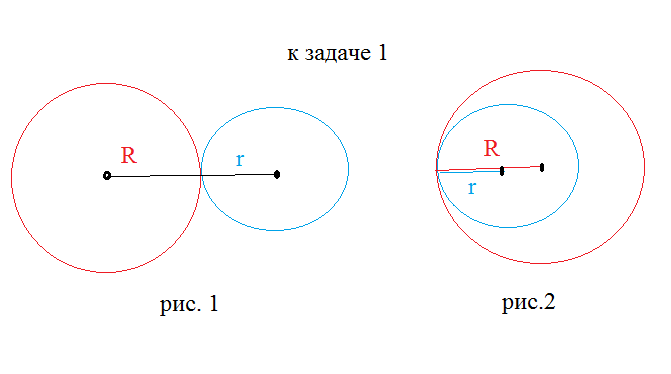
Задача 49273 1) [3 бала] Найдите расстояние между...

sofasona555

5 мая 2020 г. в 08:24

1) [3 бала] Найдите расстояние между центрами окружностей радиусов 5 м и 7 м, которые касаются:

a) внешним способом
b) внутренним способом
Для каждого случая постройте чертеж.

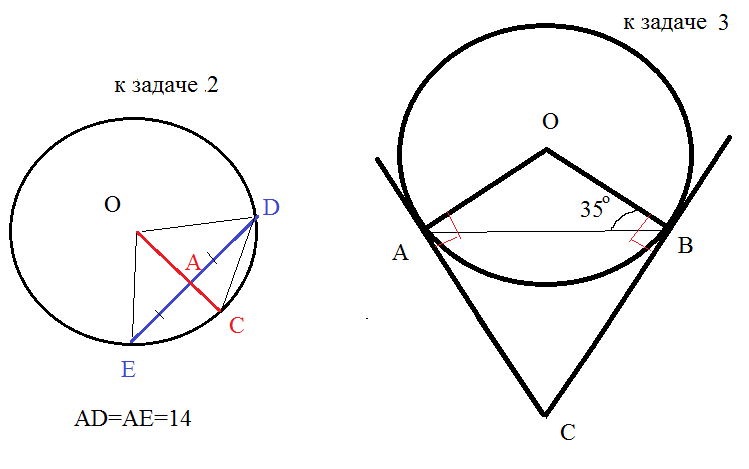
2) [3 бала] Из центра окружности О к хорде DE, равной 28 см, проведен перпендикуляр OC, который пересекает хорду в точке А. Найдите длину перпендикуляра ОА, если < ODC = 45°.

3) [4 бала] Две прямые касаются окружности с центром О в точках A и B и пересекаются в точке C. Найдите угол между этими прямыми, если < ABO = 35°.

sova

5 мая 2020 г. в 09:27

1)
а) рис 1
7+5=12
б)
рис.2
7–5=2

2)
Радиус ОС перпендикулярный хорде делит хорду пополам
AD=AE=14

Δ ODE– равнобедренный ( OD=OE=R); OC=R

∠ ODC=45 °

3)
ОА ⊥ АС
ОВ ⊥ ВС

АВ=АС

Δ АОВ – равнобедренный
рис.4