Задача 49238 Найти общее решение дифференциальных...
Условие
Важно: обязательно запишите тип каждого дифференциального уравнения!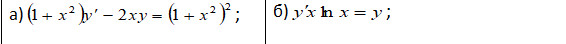
Решение
Делим обе части уравнения на (1+x^2)
Получаем
y`-(2x)/(1+x^2) * y=(1+x^2)
Можно решить двумя способами
1)Метод вариации произвольной постоянной
Решают однородное, потом константу С заменяют на C(x)
или
2)метод Бернулли
Решение неоднородного уравнения находят в виде y=u*v
y`=u`*v+u*v`
Подставляем в уравнение
u`*v+u*v`- (u*v)*2x/(1+x^2)=(1+x^2)
u`*v+u* [b](v`- 2x*v/(1+x^2)[/b]=1+x^2
Функцию v выбираем так, чтобы
[b](v`-2x*v/(1+x^2))[/b]=0
Тогда
u`*v=1+x^2
Решаем два уравнения с разделяющимися переменными
v`-2x*v/(1+x^2))=0 ⇒ dv/v=2xdx/(1+x^2) ⇒ ∫ dv/v= ∫ d(1+x^2)/(1+x^2)
ln|v|=ln|1+x^2|
v=1+x^2
u`*v=(1+x^2)
v`=1
v=x+C
y=u*v=(x+C)*(1+x^2)
[b]y=x+x^3+C(1+x^2)[/b]
б) С разделяющимися переменными
x*lnxdy=ydx
dy/y=dx/(x*lnx)
∫ dy/y= ∫ dx/(x*lnx)
ln|y|=ln|lnx|+lnc
y=C*lnx- общее решение
