Задача 49228 Решите неравенство 9^x + 54/x^2 >= ...

tunerokk

4 мая 2020 г. в 18:13

Решите неравенство 9^x + 54/x² >= 7·3^x+1/x

sova

4 мая 2020 г. в 19:07

ОДЗ: x ≠ 0

Умножаем на x² ≠ 0

9^x·x²+54 ≥ 7·x·3^x+1

3^x+1=3^x·3¹


9^x=(3²)^x=(3^x)²


(3^x)²·x²–21·(3^x)·x+54 ≥ 0

Квадратное неравенство относительно (3^x·x)

(3^x·x)²–21·(3^x·x)+54 ≥ 0

Решаем уравнение:

D=21²–4·54=441–216=225
корни:
(3^x·x)=(21–15)/2=3; 3^x·x=(21+15)/2=18
Решение неравенства:

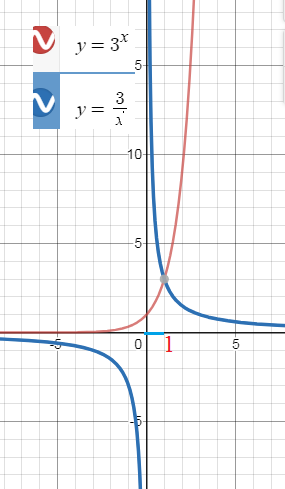
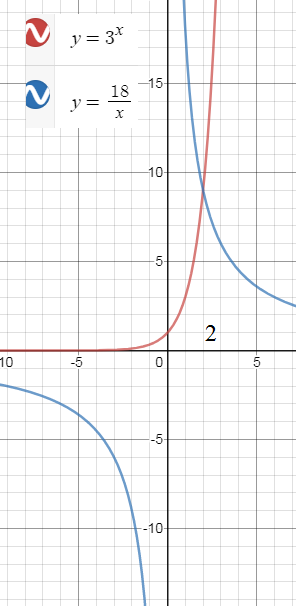
3^x ≤ 3/x или 3^x ≥ 18/x

Решаем графически:

0< x ≤ 1 ( рис.1) или x<0 или x ≥ 2

О т в е т. (– ∞; 0)U(0;1]U[2;+ ∞ )