Найдите все положительные значения а, при каждом из которых множество решений неравенства
1 ≤ (a+x2+2log5(a2–4a+5))/(30√17x4+5x2+a+1+log5 2(a2–4a+5)
состоит из одной точки, найдите это решение.
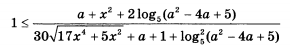
математика 10-11 класс
11528
11 февраля 2015 г. в 00:00
★
Т.к. a>0, то знаменатель положителен, умножим на него неравенство.Получим:
30·√17x4+5x2–x2+(loga2–4a+5–1)2<=0
30·x2(√17x2+5–1)+(loga2–4a+5–1)2<=0
Это возможно лишь когда оба слагаемых равны 0, сл–но х=0, a2–4a+5=5. Т.к.а>0, то а=4
Обсуждения
Вопросы к решению (6)
Обратите внимание! Данный функционал устарел, для обсуждения решений используйте функционал, вызываемый кнопкой «Обсуждения»
преобразование в первой строке решения
Откуда взялся за скобкой множитель 30, если перед х^2 его не было, и из под корня выносится только х в первой степени???
преобразования в третьей строке
преобразование в первой строке решения
Откуда взялся за скобкой множитель 30, если перед х^2 его не было, и из под корня выносится только х в первой степени???
