Задача 48799 ...
Условие
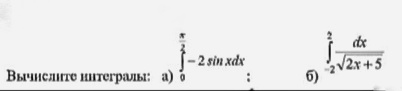
математика 10-11 класс
577
Решение
★
∫ ^(π/2)_(0)(-2sinx)dx=-2*(-cosx)|^(π/2)_(0)=2cos(π/2)-2cos0=2*0-2*1=-2
б)
Функция y=1/sqrt(2x+3) не существует в точке x=-1,5
Это несобственный интеграл второго рода.
Разбиваем область интегрирования на две области:
[-2;-1,5) и (-1,5;2]
∫ ^(-1,5)_(-2)dx/sqrt(2x+3)dx+∫ ^(2)_(-1,5)dx/sqrt(2x+3)dx=
Так как
∫ ^(-1,5)_(-2)dx/sqrt(2x+3)dx=sqrt(2x+3)|^(-1,5)_(-2)=0-1=-1
∫ ^(2)_(-1,5)dx/sqrt(2x+3)dx=sqrt(2x+3)|^(2)_(-1,5)=sqrt(2*2+3)-0=3
О т в е т. ∫ ^(-1,5)_(-2)dx/sqrt(2x+3)dx+∫ ^(2)_(-1,5)dx/sqrt(2x+3)dx= -1+3=2
