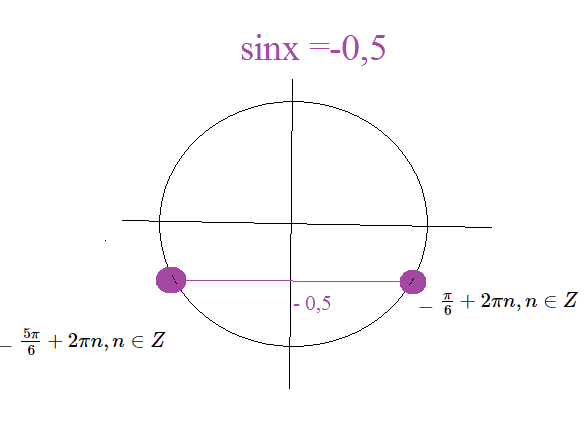Задача 48780 13 задание из ЕГЭ: а) Решите уравнение...
Условие
а) Решите уравнение -2cos^2 x=3cos(7П/2 - x)
б) Укажите корни этого уравнения, принадлежащие отрезку [5П/2; 4П]
Решение
cos((7π/2)-x)= sinx
-2cos^2x=3sinx
cos^2x=1-sin^2x
-2+2sin^2x=3sinx
Квадратное уравнение
2sin^2x-3sinx-2=0
D=25
sinx=-1/2 или sinx=2 ( это уравнение не имеет корней, |sinx| ≤ 1)
sinx=-1/2 - простейшее по формулам
[r]sinx=a
x=(-1)^(k)arcsina+πk, k ∈ Z[/r]
[m]x=(-1)^{k}arcsin(-\frac{1}{2})+\pi k, k ∈ Z[/m]
[m]arcsin(-\frac{1}{2})=-\frac {\pi}{6}[/m], так как [m] sin(-\frac {\pi}{6})=-\frac{1}{2}[/m] и [m]-\frac {\pi}{6}\in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
[m]x=(-1)^{k}(-\frac{\pi}{6})+\pi k, k ∈ Z[/m]
при k=2n
получаем
[m]x=-\frac{\pi}{6}+ 2\pi n, n ∈ Z[/m]
при k=2n+1
получаем
[m]x=\frac{\pi}{6}+ \pi +2\pi n=\frac{7\pi}{6}+2\pi n, n ∈ Z[/m]
или
[m]x=-\frac{5\pi}{6}+2\pi n, n ∈ Z[/m]
см. рис. 1
Отрезку [5π/2; 4π]
принадлежат корни:
[m]-\frac{\pi}{6}+ 2\pi =\frac{11 \pi}{6}[/m]
[m]-\frac{5\pi}{6}+ 2\pi =\frac{7 \pi}{6}[/m]