Задача 48687 ПОМОГИТЕ С ПОДРОБНЫМ РЕШЕНИЕМ...

vk396216921

2020-04-28 13:43:43

ПОМОГИТЕ С ПОДРОБНЫМ РЕШЕНИЕМ ПОЖАЛУЙСТА.
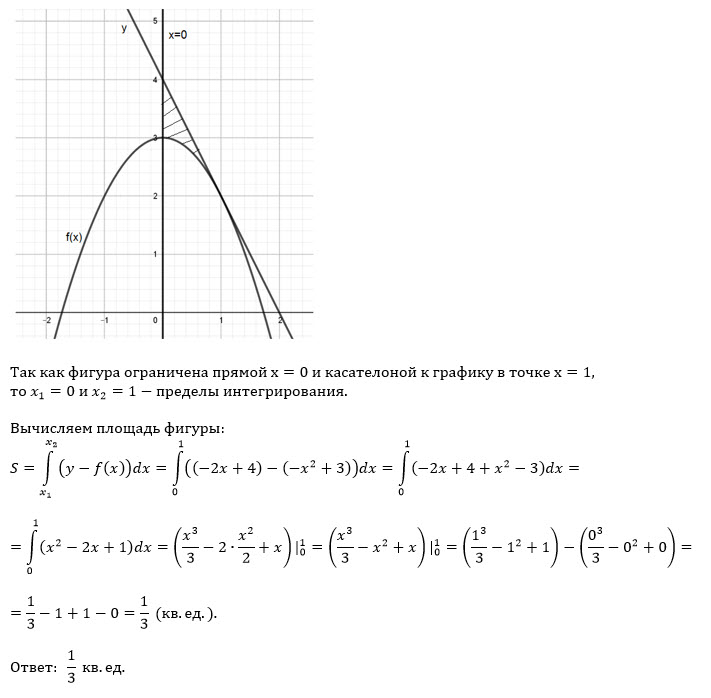
1)Вычислите площадь фигуры, ограниченной графиком функции у=-х^2+3, касательной к этому графику в его точке с абсциссой х=1 прямой х=0.
2) Найдите ту первообразную функции f(x)=2x+5, для графика которой прямая у=7х-3 является касательной.

sova

2020-04-28 13:53:43

1.
Написать уравнение касательной.
y–f(xo)= f `(xo)·(x–xo)

f (x) = – x^2+3
f (xo) = f(2)=-(2^2)+3=-1

f `(x) = –2x

f`(xo)=f `(2)=-2*2=-4

y- (-1)=-4*(x-1) ⇒ y=-4x+3

S= ∫ ^(1)_(0) ((-4x+3) –(-x^2+3)) dx=...


2.


F(x) – первообразная, значит F`(x)=f(x)


y=7x–3 – касательная к F(x) это прямая вида y=kx+b
k=7
b=–3

Написать уравнение касательной для F(x) в точке xo
(точка неизвестна, ее нам надо найти)

y – F (xo)= F `(xo)·(x–xo)
запишем в привычном виде:

y=F `(xo)·x + F (xo) – F `(xo)·xo – это прямая вида

y=kx+b

k=F `(xo)

b= F (xo) – F `(xo)·xo


F`(x)=f(x)=2x+5

7=2xo+5 ⇒ xo=1

yo=?