Задача 48659 В правильной шестиугольной призме А......
Условие
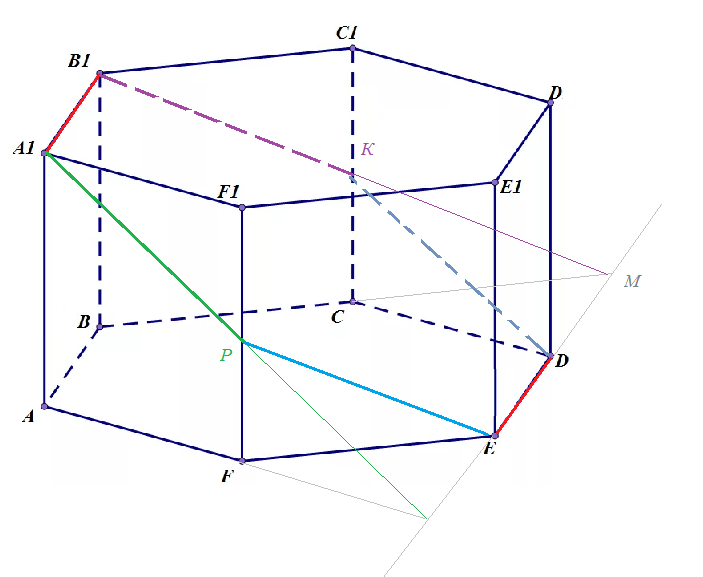
а) постройте сечение призмы плоскостью, проходящей через точки D, E и А1.
б) найдите расстояние от тоски А до плоскости DEA1
Решение
В верхнем проходит через точку А_(1)
Основания параллельны между собой. Поэтому если секущая плоскость пересекает и верхнее и нижнее основания, то линия пересечения секущей плоскости с верхним основанием || прямой DE.
Такой прямой в верхнем основании, проходящей через точку A_(1)
является А_(1)B_(1)
Проекция точки В_(1) - точка В продолжаем ребро ВС до пересечения с DE. Получаем точку M.
Cоединяем точку М с точкой В_(1). Прямая B_(1) M пересекает ребро CC_(1) в точке К
Аналогично строим точку P на ребре FF_(1)
Сечение A_(1)PEDKB_(1) - искомое сечение.
2.
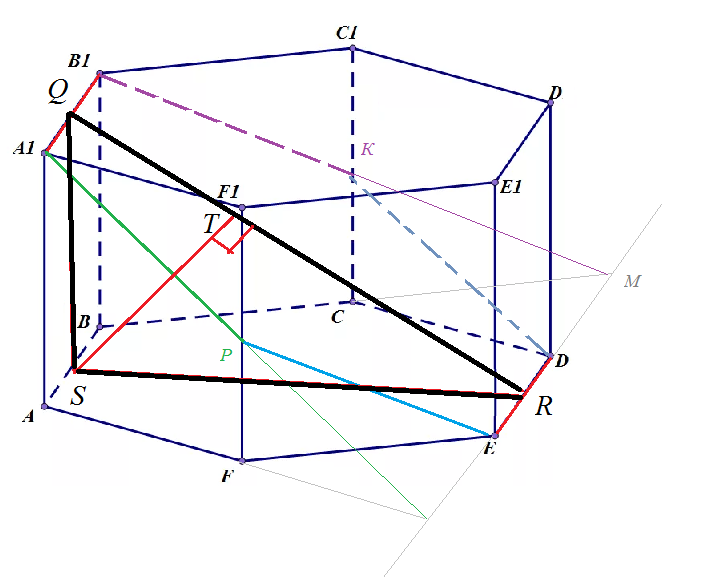
Расстояние от точки А равно расстоянию от точки S, где S - cередина АВ.
SТ ⊥ QR
SТ - высота прямоугольногго треугольника SQR
SQ=AA_(1)=1
SR=2*1=2
SR=sqrt(1+2^2)=sqrt(5)
ST=1*2/sqrt(5)
S=a*b/2; S=c*h/2 ⇒ a*b=c*h ⇒ h=a*b/c
a, b - катеты
с- гипотенуза
h- высота к гипотенузе.