Задача 48577 1% 100 $ купюр составляют фальшивые,...

g_group

2020-04-27 17:06:37

1% 100 $ купюр составляют фальшивые, сделанные
довольно искусно, так что операцийник обменного пункта десятую
их часть принимает за настоящие. Каждый день для обмена
приносят примерно 200 100$ купюр (всех настоящих и
фальшивых). Определить: 1) вероятность того, что среди них есть хотя
бы 1 фальшивая; 2) наиболее вероятное время, за которое оправдает себя
детектор валют, который стоит 100 $ и определяет все фальшивые
купюры как фальшивые.
Варианты ответов: 1) а) 0,245 б) 0,107; в) 0,154 г) 0,203,
2) а) 5 дней. б) 7 дней в) 14 дней, г) 11
дней.

sova

2020-04-27 19:43:17

★

Вероятность появления события А в одном испытании равна p.
Тогда вероятность появления события А в серии из n испытаний ровно m раз найдем по формуле Пуассона:

P_(k)(m)=[m]\frac{k^{m}\cdot e^{-k}}{m!}[/m]

(если n - велико, p очень мало)

n=200
p=0,01


k=np=200*0,01=2

Найти P_(k) (m ≥ 1)

Найдем вероятность противоположного события

Ни одной фальшивой купюры:

P_(k) (m=0)


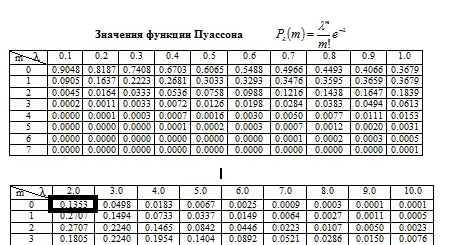
P_(k)(m=0)= [m]\frac{2^{0}\cdot e^{-2}){0!}[/m]≈ 0,1353

( cм . приложение. Таблица значений)

Тогда P_(200)(m ≥ 1)=1-P_(200)(m=0)=1-0,1353=0,8643