Задача 4854 Острые углы прямоугольного треугольника...

ElizavettaKoshkovatova

30 октября 2015 г.

Острые углы прямоугольного треугольника равны 63° и 27°. Найдите угол между биссектрисой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

По рисунку видим, что CM – медиана, CD – биссектриса. Пусть угол A равен 27, а угол B равен 63.
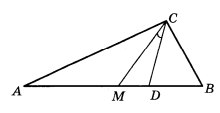
Так как, медиана прямоугольного треугольника, опущенная из вершины прямого угла, равна половине его гипотенузы, то AM = MC. И треугольник AMC – равнобедренный. А в равнобедренном треугольнике углы при основании равны.
<MAC=<MCA=27
CD – биссектриса: <ACD=90/2=45
<MCD=<ACD–<ACM=45–27=18

Ответ: 18