Задача 48470 Помогите плисс...
Условие
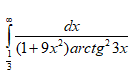
Решение
d(arctg 3x)==[m]\frac{3}{1+(3x)^2}dx[/m]
Несобственный интеграл первого рода с бесконечным верхним пределом.
Применяем формулу Ньютона-Лейбница
∫ ^(+ ∞ )_(a)f(x)dx=F(x)|^(+ ∞ )_(a)=F(+ ∞ )-F(a),
где F(+ ∞ )=lim_(x → + ∞ )F(x)
[m] \int ^{+\infty}_{\frac{1}{3}} \frac{dx}{(1+9x^2)\cdot arctg^23x}=
\frac{1}{3}\int ^{+\infty}_{\frac{1}{3}} \frac{d(arctg3x)}{arctg^23x}dx=[/m]
[m]=\frac{1}{3}\int ^{+\infty}_{\frac{1}{3}} arctg^{-2}3x d(arctg 3x)=[/m]
[m]=\frac{1}{3}(-\frac{1}{arctg3x})|^{+\infty}_{\frac{1}{3}}=[/m]
F(+ ∞ )=lim_(x → + ∞ )F(x)
arctg(+ ∞ ) = lim_(x → + ∞ )arctg3x=[m]\frac{\pi}{2}[/m]
[m]=-\frac{1}{3}\cdot\frac{1}{\frac{\pi}{2}}+\frac{1}{3}\cdot \frac{1}{arctg1}=[/m]
arctg1=[m]\frac{\pi}{4}[/m]
[m]=-\frac{2}{3 \pi}+\frac{4}{3 \pi}=\frac{2}{3 \pi}[/m]