Задача 48358 Боковое ребро правильной треугольной...

slava191

2020-04-25 16:05:37

Боковое ребро правильной треугольной призмы на 20% больше ее стороны основания. Расстояние между серединами двух непараллельных ребер, принадлежащих разным основаниям, равно 13. Найдите площадь боковой поверхности призмы. (ларин 8)

sova

2020-04-25 17:32:59

★

Пусть сторона основания равна [b]x[/b]. Тогда боковое ребро равно
[b]1,2*x[/b].

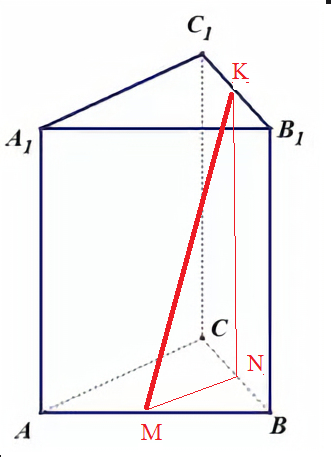
MK- расстояние между серединами двух непараллельных ребер, принадлежащих разным основаниям.

MN- проекция MK на плоскость основания АВС.

MN - средняя линия треугольника АВС.

MN=x/2

По теореме Пифагора из треугольника МКN

MK^2=MN^2+NK^2

13^2=(x/2)^2+(1,2x)^2

169=1,69x^2

x^2=100

x=10

Сторона основания равна 10, высота призмы 12.

S_(бок)=P_(осн)*Н=(10+10+10)*12=360

О т в е т.[b] 360.[/b]