Задача 48324 Боковое ребро правильной...

vk361563663

2020-04-25 14:52:39

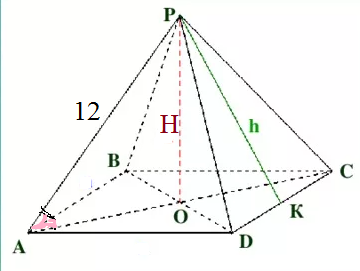
Боковое ребро правильной четырехугольной пирамиды равно 12 см и образует с плоскостью основания пирамиды угол 45°.
а) Найдите высоту пирамиды.
б) Найдите площадь боковой поверхности пирамиды.

sova

2020-04-26 23:17:45

∠ PAO=45 ° ⇒ ΔPAO - прямоугольный равнобедренный.

а)[b]H[/b]=PO=AO=12*sin45 °12*sqrt(2)/2[b]=6sqrt(2)[/b]

AO=AC/2

AC=2AO=12*sqrt(2) ⇒ Из Δ АСD:

AD=12sqrt(2)*sin45 ° =[b]12[/b]

Апофема боковой грани:
h^2=PD^2-DK^2=(12)^2-6^2=144-36=108
h=sqrt(108)=6sqrt(3)

б) S=P_(осн)*h/2=(4AD)*h/2=2AD*h=[b]24*6sqrt(3)[/b]