Задача 48287 2. Нормально распределенная с. в. X...

vk305708338

2020-04-25 10:06:13

2. Нормально распределенная с. в. X задана плотностью вероятностей

[m] f(x) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{x^2}{2}}. [/m]

Найти: а) вероятность попадания с. в. в интервал (1,3); б) симметричный относительно математического ожидания интервал, в который с вероятностью 0,8926 попадет с. в. X в результате опыта; в) [m] M_0 X [/m] и [m] M_e X [/m]. Построить нормальную кривую f(x).

sova

2020-04-25 11:54:01

★

N(0;1) ⇒ m=0; σ =1

P( α <X< β )=Ф( ( β -m)/ σ )- Ф(( α -m)/ σ )

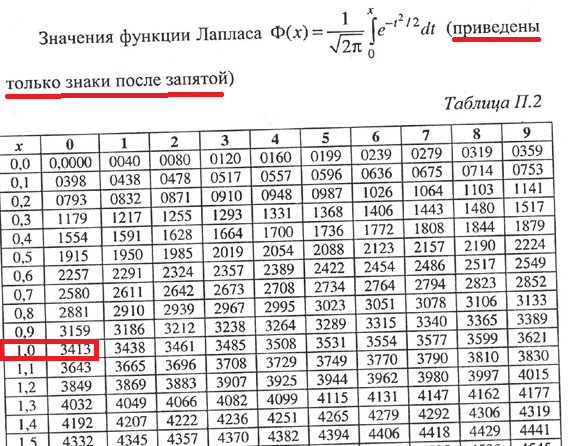
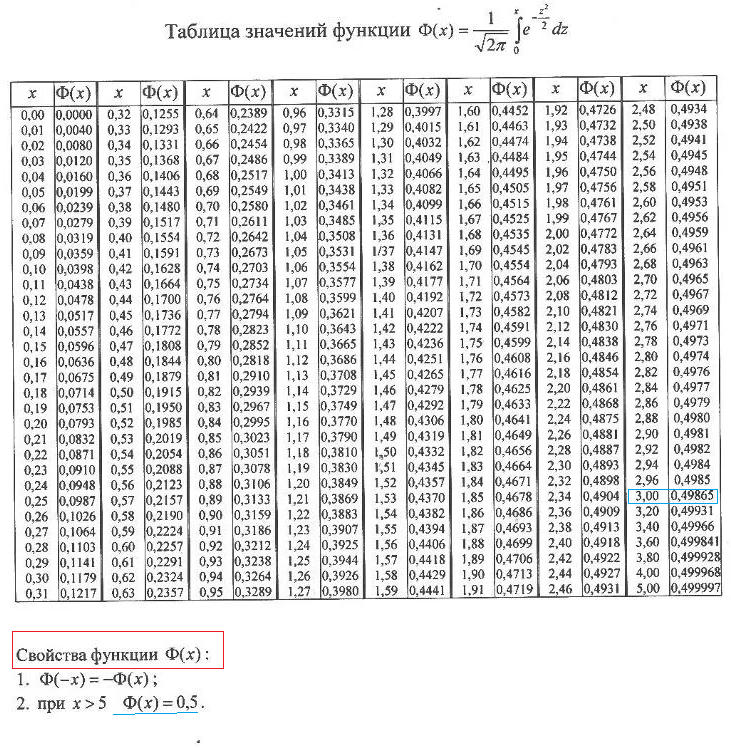
[b]Значения функции Ф(х) в таблице.[/b]

а)

P( 1 <X< 3 )
α =1
β =3
( β -m)/ σ=(3-0)/1=3
( α -m)/ σ=(1-0)/1=1

Cм таблицу ( рисунок)

Ф(1)=0,3413

Ф(3)= 0,49865


P( 1 <X< 3 )=Ф(3)-Ф(1)=0,49865-0,3413=считаем...

Кривая на рис.