Задача 48247 4y3y''=y4–1, y(0)=корень из 2, y'(0)=1...
Условие
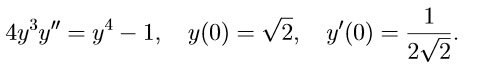
Решение
y`(x)=z(y)
y``=z`(y)*y`(x)=z`(y)*z
подставляем в уравнение:
4y^3*(z`(y)*z)=y^4-1
и получаем уравнение первого порядка, неизвестной функцией является z(y)
так как z`(y)=dz/dy, то
4y^3*(z*dz/dy)=y^4-1 - уравнение с разделяющимися переменными
z*dz=(y^4-1)dy/4y^3
Интегрируем:
∫ zdz=(1/4) ∫ (y^4-1)dy/y^3
Cправа делим почленно на y^3
z^2/2=(1/4) ∫ (y^4dy/y^3)-(1/4) ∫ (dy/y^3)
z^2/2=(1/4) ∫ ydy-(1/4) ∫ y^(-3)dy
z^2/2=(1/4) * (y^2/2)-(1/4) ( y^(-2)/(-2) + c_(1)
⇒ z^2=(1/4)y^2+(1/4)*(1/y^2)+C_(1); C_(1)=2c_(1)
z=sqrt((1/4)y^2+(1/4)*(1/y^2)+C_(1))
и возвращаемся к замене:
y`(x)=z(y)
y`(x)= sqrt((1/4)y^2+(1/4)*(1/y^2)+C_(1))
y`=dy/dx
dy/dx=sqrt((1/4)y^2+(1/4)*(1/y^2)+C_(1))
dy/sqrt((1/4)y^2+(1/4)*(1/y^2)+C_(1))=dx
(1/4)y^2+(1/4)*(1/y^2)=((1/2)y+(1/2)*(1/y))^2-1/2
dy/sqrt(((1/2)y+(1/4)*(1/y))^2+C_(1)-(1/2))=dx
Интегрируем...
Но это не просто...
Возвращаюсь к условию
4y^3* y``=y^4-1
Если
u=y^4-1
то
u`=4y^3*y`
Уравнение принимает вид:
(u`*y`)*y``=u
y``=(y`)`
(u`*y`)*(y`)`=u
Может быть воспользоваться тем, что
[b]y`_(x)=1/(x`_(y))
[/b]
