Задача 47721 Окружность радиусов 2 и 3 касаются...

hikari2ai

2020-04-20 20:13:40

Окружность радиусов 2 и 3 касаются внутренним образом. Найти радиус третьей окружности, касающейся первых двух и линии их центров

sova

2020-04-20 21:29:23

Обозначим центр большой окружности О, её радиус R=3
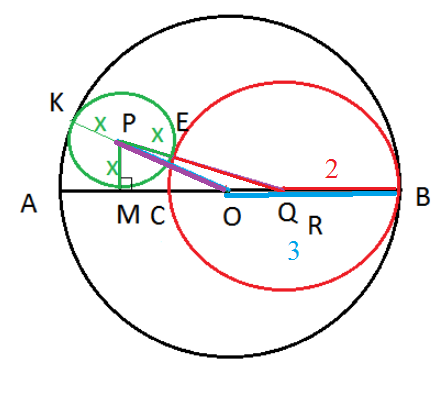
Центр окружности, касающейся большой окружности внутренним образом Q, её радиус r=2,
центр третьей окружности, касающейся этих двух Р, радиус х.
См. рисунок.
Рассмотрим треугольник POQ.
Прямая, соединяющая центры касающихся окружностей проходит через точку касания.
АВ- линия центров окружностей, касающихся внутренним образом, проходит через точки О и Q.
AB=6; CD=4 ⇒ OQ=OB-QB=3-2=1.
РО=3-x
PQ=2+x



б)Рассматриваем два прямоугольных треугольника.
МРО и МРQ.
М- точка касания третьей окружности с линией центров первых двух.
Значит РМ⊥АВ.

Находим МО по теореме Пифагора из Δ МРО:
МО^2=PO^2-PM^2=(3-x)^2-x^2 ⇒
МО= sqrt(9-6x)

Находим МQ по теореме Пифагора из Δ МРQ:
МQ^2=PQ^2-PM^2=(2+x)^2-x^2 ⇒
МQ= sqrt(4+4x)

Так как MQ=MO+OQ, приравнивая получаем иррациональное уравнение:
sqrt(4+4x)=sqrt(9-6x)+ 1.

Возводим в квадрат.
4+4x=9-6x+2sqrt(9-6x)+1
sqrt(9-6x)=5x-3

Возводим в квадрат.
9-6x=25x^2-30x+9

25x^2-24x=0
x=0,96 или х=0- не удовл. условию задачи
О т в е т. [b]0,96[/b]