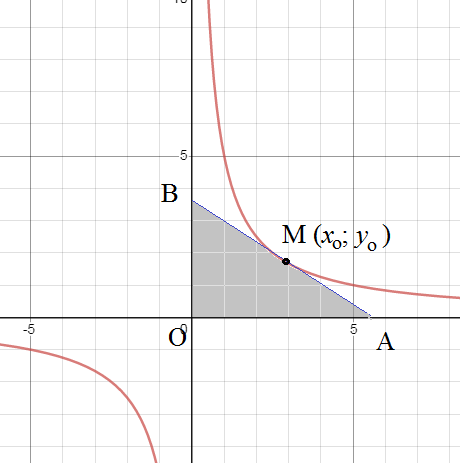Задача 47674 ...

vk585844076

20 апреля 2020 г. в 15:11

♦44.69. Докажите, что треугольник, образованный касательной
к гиперболе у = a²/x и осями координат, имеет постоянную
площадь, а точка касания является центром окружности,
описанной около этого треугольника. Рассмотрев чертеж
к задаче, придумайте геометрический способ построения
касательной к гиперболе.

sova

20 апреля 2020 г. в 15:48

[m]M (x_{o};\frac{a^2}{x_{o}})[/m] – точка касания.

[m]f `(x)=-\frac{a^2}{x^2}[/m]

[m]f `(x_{o})=-\frac{a^2}{x^2_{o}}[/m]

Уравнение касательной:

[m]y=\frac{a^2}{x_{o}}-\frac{a^2}{x^2_{o}}\cdot (x-x_{o})[/m]

Находим координаты точек пересечения касательной с осью ОХ:
А(x_A;0)

[m]\frac{a^2}{x_{o}}-\frac{a^2}{x^2_{o}}\cdot (x-x_{o})=0[/m] ⇒ x_A=

с осью ОY:

B(0;y_B)

[m]y=\frac{a^2}{x_{o}}-\frac{a^2}{x^2_{o}}\cdot (0-x_{o})[/m] ⇒ y_B=


S _Δ=OA·OB/2=x_Ay_B/2= ...