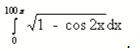
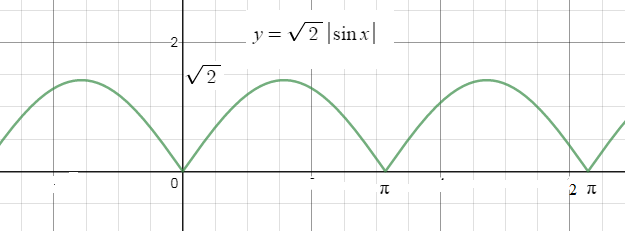Задача 47580 Вычислить интеграл ...

bratish444

2020-04-19 20:09:36

Вычислить интеграл

sova

2020-04-19 20:20:20

Формула:
1-cos2x=2sin^2x

∫ ^([b]100π[/b])_(0)sqrt(2sin^2x)dx=[red]sqrt(2)[/red] ∫ ^(100π)_(0) |sinx|dx=

=[red]sqrt(2)[/red]* (100∫ ^([b]π[/b])_(0) sinx+ 100∫ ^([b]2π[/b])_(π)(-sinx)dx)=

=[red]sqrt(2)[/red]*(100 (-cosx)|^(π)_(0)+100*(cosx)|^(2π)_(0))=

=[red]sqrt(2)[/red]*(100*(-(-1)+1)+100*(1-(-1)))=[b]400sqrt(2)[/b]