Задача 47571 ...
Условие
1. Докажите, что грань BB1C1C — прямоугольник.
2. Вычислите площадь грани AA1B1B.
3. Вычислите площадь поверхности призмы.
4. Составьте план вычисления объёма призмы.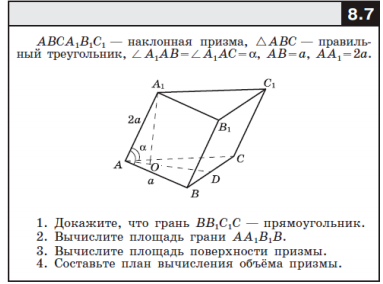
Решение
ВВ_(1)||СС_(1)
B_(1)C_(1)|| BC
ВВ_(1)С_(1)С - параллелограмм,
Чтобы доказать, что это прямоугольник надо доказать, что хотя бы один угол прямой. СМ приложение.
2.
AA_(1)B_(1)B - параллелограмм, площадь параллелограмма
S_(параллелограмма)=a*b*sin α
S_(AA_(1)B_(1)B)=AA_(1)*AB*sin α =2a*a*sin α =[b]2a^2*sin α [/b]
3.
S_(поверхности)=2S_(осн)+[b]S_(AA_(1)B_(1)B)[/b]+[b]S_(AA_(1)C_(1)C)[/b]+
S_(BB_(1)C_(1)C)=
=2*(a^2sqrt(3)/4) + [b]2a^2*sin α [/b]+[b]2a^2*sin α [/b]+2a*a=
4.
Найти S_(осн) - см. пункт 3
Найти A_(1)O- высоту призмы
V=S_(осн) *A_(1)O
