Задача 47502 Помогите пожалуйста решить ...
Условие
математика
439
Решение
★
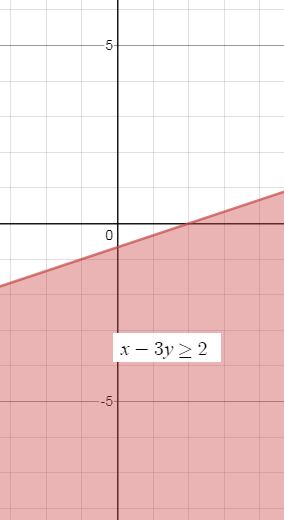
x+3y=2- это прямая
Для ее построения достаточно двух точек:
(2;0);(-1;1)
Эта прямая разделила плоскость на две части ( cм рис. 1)
Выбираем любую точку плоскости, например (0;0)
Подставляем в первое неравенство:
0-3*0 ≥ 2 - неверно
Значит область, задаваемая первым неравенством та, в которой нет точки (0;0)
Аналогично поступаем со вторым неравенством
(см. рис.2)
2x-y <3
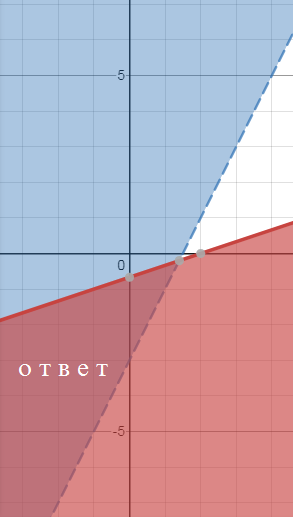
Неравенство строгое. Поэтому границу рисуем [b]пунктирной[/b] линией , проходящей через точки:
(0;-3) (2;1)
Cистеме неравенств удовлетворяет пересечение областей
(см. рис.3)- область темного цвета
Одна граница сплошная линия, вторая - пунктирная.
