Задача 47477 13 задание ЕГЭ, нужна помощь!...
Условие

Все решения
{cosx ≠ 0
{2*(1-sin^2x)+3sinx-3=0
{cosx ≠ 0
{2sin^2x-3sinx+1=0
{cosx ≠
{D=9-8=1; sinx=1 или sinx=0,5
{cosx ≠ 0
sinx=1 не удовлетворяет второму условию, так как если sinx=1, cosx=0 (так как sin^2x+cos^2x=1)
sinx=0,5
Решаем по формуле:
[r]sinx=a ⇒ x=(-1)^(k)arcsina+πk, k ∈ Z[/r]
[m]x=(-1)^{k}arcsin\frac{1}{2}+\pi k, k ∈ Z[/m]
[m]arcsin\frac{1}{2}=\frac {\pi}{6}[/m], так как [m] sin\frac {\pi}{6}=\frac{1}{2}[/m] и [m]\frac {\pi}{6}\in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
[m]x=(-1)^{k}\frac{\pi}{6}+\pi k, k ∈ Z[/m]
при k=2n
получаем
[m]x=\frac{\pi}{6}+ 2\pi n, n ∈ Z[/m]
при k=2n+1
получаем
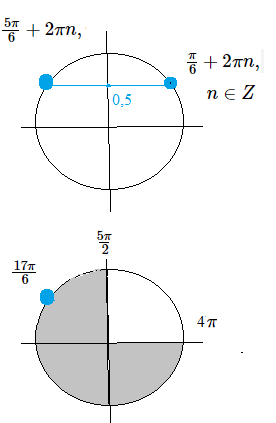
[m]x=-\frac{\pi}{6}+ \pi +2\pi n=\frac{5\pi}{6}+2\pi n, n ∈ Z[/m]
Тогда легко отобрать корни:
[m]\frac{5\pi}{6}+2\pi=\frac{17\pi}{6}[/m]
----------------------------
О т в е т.
а) [m]\frac{\pi}{6}+ 2\pi n, n ∈ Z[/m][m]\frac{5\pi}{6}+2\pi n, n ∈ Z[/m]
б)[m]\frac{17\pi}{6}[/m]