Задача 47461 Вычислить двойной интеграл, используя...
Условие
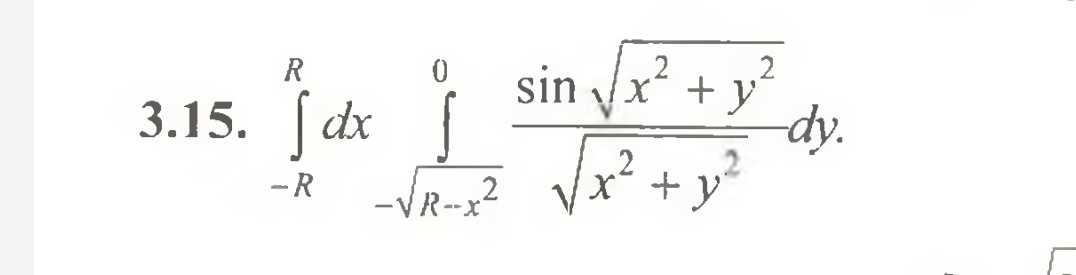
предмет не задан
1352
Все решения
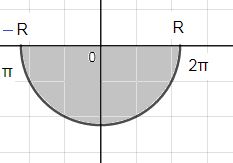
y=r*sin φ
0 ≤ r ≤ R
π ≤ φ ≤ 2π
dxdy=r* drd φ
x^2+y^2=r^2
= ∫ ^(2π)_(π)d φ ∫ ^(R)_(0) ( sinr/r)* r dr=
=∫ ^(2π)_(π)d φ ∫ ^(R)_(0) sinr dr=
=(-cosR+cos0)*(2π-π)=[b]π*(1-cosR)[/b]