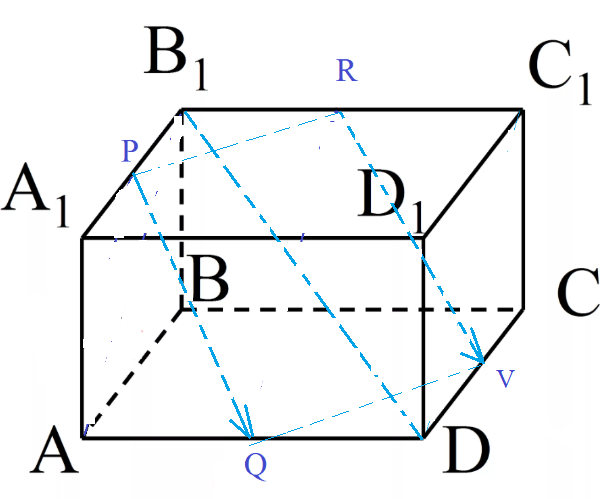
Задача 47363 На рёбрах [m]A_1B_1[/m], AD,...

nomi20

2020-04-16 16:30:14

На рёбрах [m]A_1B_1[/m], AD, [m]B_1C_1[/m], CD и [m]AA_1[/m] параллелепипеда [m]ABCDAB_1C_1D_1[/m] взяты точки [m]P[/m], [m]Q[/m], [m]R[/m], [m]V[/m] и [m]A_2[/m] соответственно - середины этих рёбер. Укажите сонаправленные векторы в каждой из следующих троек векторов:

[m]
\overrightarrow{PQ}, \overrightarrow{B_1D} и \overrightarrow{RV}
[/m]

sova

2020-04-16 17:39:16

★

QPRV -[b]параллелограмм[/b]
так как
PR|| A_(1)C_(1)
PR=(1/2) A_(1)C_(1)

QV|| AC
PR=(1/2) AC

AC=A_(1)C_(1)

vector{PQ} и vector{RV} как стороны параллелограмма
QPRV