Задача 47275 Решить дифференциальные...
Условие
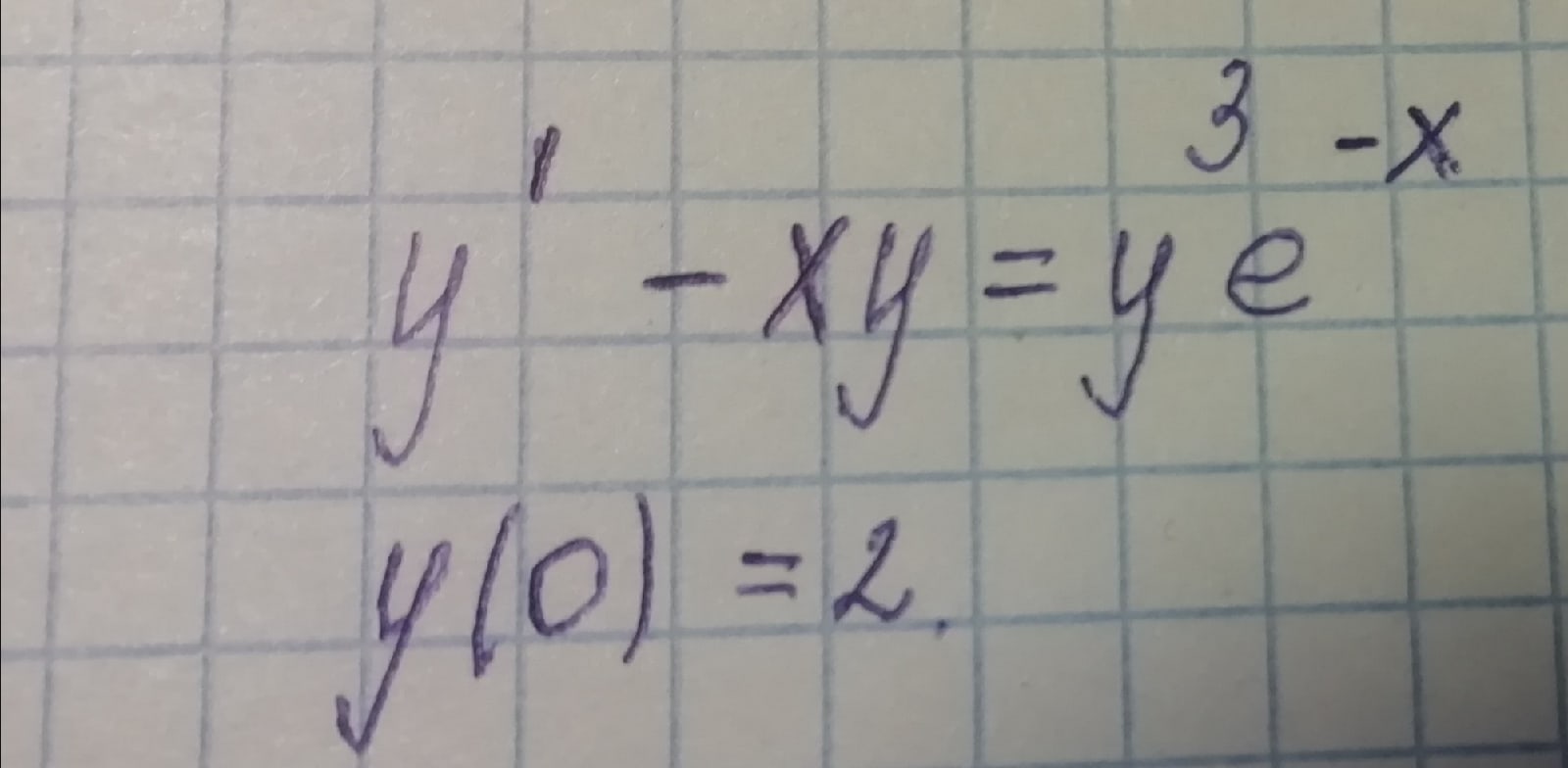
математика
901
Все решения
n=3
Решаем методом Бернулли.
Решение в виде
y=u*v
Находим
y`=u`*v+u*v`
Подставляем в уравнение:
u`*v+u*v`-x*u*v=(u*v)^3*e^(-x)
u`*v+u[b](v`-x*v[/b])=(u*v)^3*e^(-x)
Выбираем функцию v так,чтобы
[b]v`-x*v[/b]=0
Решаем уравнение с разделяющимися переменными
[b]v`-x*v=0 [/b]⇒ dv/dx=x*v⇒ dv/v=xdx ⇒ ∫ dv/v=∫ xdx ⇒ ln|v|=x^2/2 ⇒ [blue]v=e^(x^2/2)[/blue]
Тогда данное уравнение принимает вид
u`[blue]*e^(x^2/2)[/blue]+0=(u)^3*([blue]e^(x^2/2)[/blue])^3*e^(-x)
u`=u^3*e^(x^2)*e^(-x)
u`=du/dx
du/u^3=e^(x^2-x)dx
Интегрируем: