Задача 47106 Вычислить площадь поверхности шара,...

kodzimageniy

2020-04-14 18:55:13

Вычислить площадь поверхности шара, вписанного в конус, если образующая конуса равна 9 см, высота конуса равна 7,2 см. (Если в промежуточном ответе большое количество знаков после запятой, округляй ответ до сотых.)

sova

2020-04-14 19:06:58

★

Шар вписан в конус ⇒ в осевое сечение конуса, вписана окружность

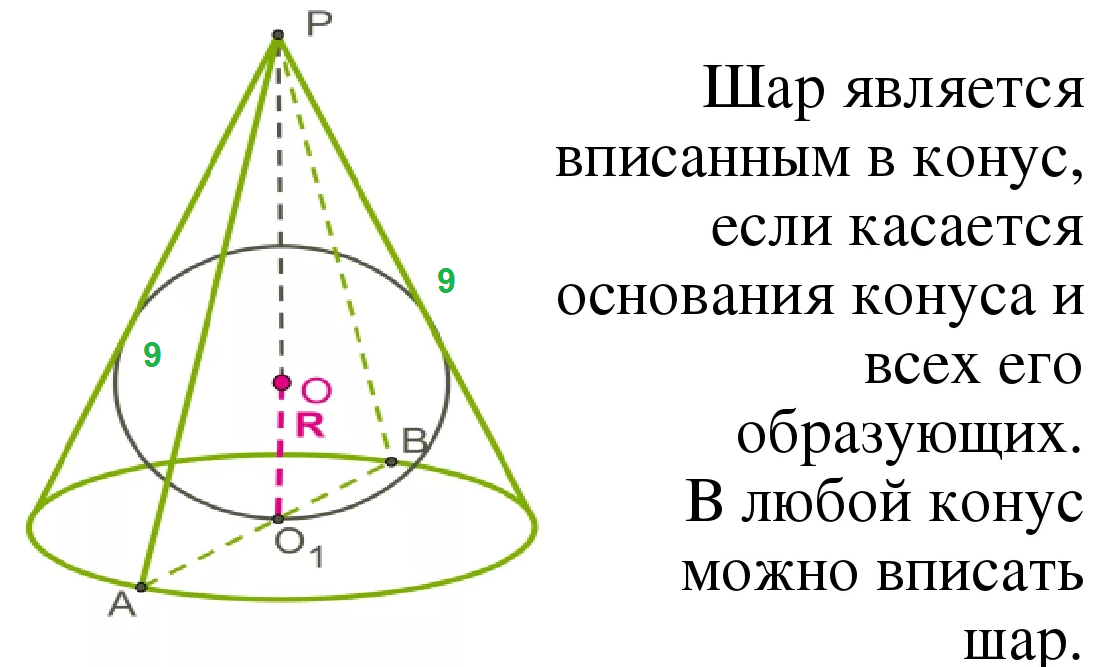
Осевое сечение - равнобедренный треугольник,
боковые стороны 9, высота, 7,2
Найдем AO_(1)

АО^2_(1)=9^2-7,2^2=(9-7,2)*(9+7,2)=1.8*16.2

AO_(1)=5,4

AB=10,8

P=9+9+10,8=28,8

p=P/2=14,4

S_( Δ PAB)=(1/2)AB*PO_(1)=(1/2)*10,8*7,2

[b]r_(шара)=S_(Δ PAB)/p[/b]=(5,4*7,2)/14,4=5,4/2=[b]2,7[/b]

S_(пов. шара)=4πr^2=4π*(2,7)^2=[b]29,16π[/b]