Задача 47063 |x-1| + |2x-6| < 5...

vk384750626

2020-04-14 12:48:21

|x-1| + |2x-6| < 5

sova

2020-04-14 22:02:25

[i]Подмодульные [/i]выражение обращаются в ноль в точках:

x=1 и х=3

Эти точки разбивают числовую прямую на три промежутка.
Раскрываем модули на этих промежутках:

1) x ≤[b] 1[/b]
|x-1|=-x+1
|2x-6=-2x+6
Неравенство принимает вид:
-x+1-2x+6<5
-3x<-2 - верно
Значит x >2/3

решение (2/3;[b]1[/b]]

2) 1 < x ≤ 3
x-1-2x+6<5
-x<0 ⇒ x>0

решением неравенства является (1;3]

3) x > 3
х-1+2х-6 <5

3x<12

x<4

Решение (3;4)

Объединяем ответы трех случаев:

(2/3;1]U(1;3]U(3;4)=[b](2/3;4)
[/b]

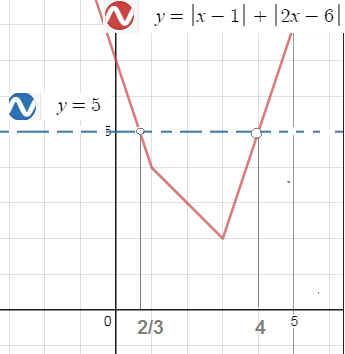
Второй способ [i]Графическое решение[/i]