Задача 47029 исследовать сходимость несобственного...
Условие
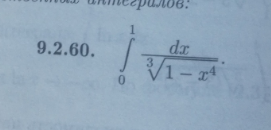
Все решения
Особая точка x=1,
По определению
[m]\int^{1}_{0}\frac{dx}{\sqrt[3]{1-x^4}} =\lim_{\varepsilon\to 0}\int^{1-\varepsilon }_{0}\frac{dx}{\sqrt[3]{1-x^4}}[/m]
[m]\int\frac{dx}{\sqrt[3]{1-x^4}}[/m] - неопределенный интеграл от иррациональной функции.
Можно сделать замену
x^2=sint
x=sqrt(sint)
dx=[m]\frac{(sint)`dt}{2\sqrt{sint}}[/m]
[m]\int\frac{dx}{\sqrt[3]{1-x^4}}=\int\frac{\sqrt[3]{cost}dt}{2\sqrt{sint}}[/m]
Скорее всего применение теорем.
Например, теорему сравнения:
[m]\sqrt[3]{1-x^4}=\sqrt[3]{(1-x^2)(1+x^2)}=\sqrt[3]{(1-x)(1+x)(1+x^2)}[/m]
По крайней мере степень уменьшится.
так как множитель (1+x)(1+x^2) в точке x=1 не имеет особенностей
Осталось исследовать
[m]\int\frac{dx}{\sqrt[3]{1-x}}[/m]
Вот его по определению вычислить проще:
[m]\int^{1}_{0}\frac{dx}{\sqrt[3]{1-x}} =\lim_{\varepsilon\to 0}\int^{1-\varepsilon }_{0}\frac{dx}{\sqrt[3]{1-x}}=[/m]
[m]\lim_{\varepsilon\to 0}\int^{1-\varepsilon }_{0}(1-x)^{-\frac{1}{3}}dx=[/m]
[m]=-\lim_{\varepsilon\to 0} \frac{(1-x)^{-\frac{1}{3}+1}}{-\frac{1}{3}+1}|^{1-\varepsilon }_{0}=\frac{3}{2}[/m]
Сходится по теореме сравнения
[m]g(x)=\frac{1}{\sqrt[3]{1-x}}> \frac{1}{\sqrt[3]{1-x^4}}=f(x)[/m]