Задача 47 Прибор наблюдения обнаружил летящий...
Условие
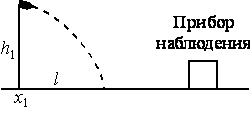
Все решения
=> cosA = L/Vt;
Известно, что общая дальность полёта (а нам её и надо найти) - это V*cosA * t полёта.
Известно всё, но не время.
По вертикали действует ускорение g. Уравнение скорости по вертикальной оси: B = VsinA - gt.
На "самом верху" скорость будет равна нулю. Значит для того, чтобы добраться туда, нужно потратить время t = VsinA / g. На падение тело потратит то же время, а значит время продолжительности полёта есть 2t = 2 * V * sinA / g
Подставим t в формулу V * cosA * t = 2 * V^2 * sinA * cosA / g
cos уже считали. А синус связан с ним тригонометрическим тождеством (sin^ + cos^2 = 1)
Тогда S = 2 * V * L * sqrt(1 - (L/Vt)^2) / gt
Вроде так...