Задача 46788 ...

azot

2020-04-12 18:14:59

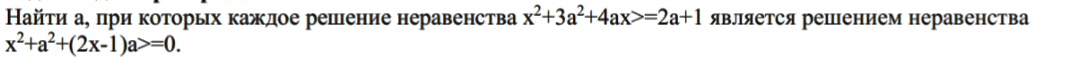
Найти а, при которых каждое решение неравенства x²+3a²+4ax≥2a+1 является решением неравенства x²+a²+(2x-1)a≥0

sova

2020-04-12 21:41:24

★

Перепишем каждое неравенство как квадратное относительно x

Первое:
x^2+3a^2+4ax-2a-1 ≥ 0

x^2+4ax+(3a^2-2a-1) ≥ 0

D=(4a)^2-4*(3a^2-2a-1)=16a^2-12a^2+8a+4=4a^2+8a+4=4*(a+1)^2

sqrt(D)=2(a+1)

x_(1)=-2a-(a+1)=-3a-1; x_(2)=-2a+(a+1)=3a+1

Решение первого неравенства:

x ≤-3a-1 или x ≥ 3a+1

Второе:
x^2+a^2+2ax-a ≥ 0

x^2+2ax+(a^2-a) ≥ 0

D=(2a)^2-4*(a^2-a)=4a^2-4a^2+4a=4a

sqrt(D)=2sqrt(a)

x_(3)=-a-sqrt(a); x_(4)=-a+sqrt(a)

Решение второго неравенства:

x ≤-a-sqrt(a) или x ≥ -a+sqrt(a)


каждое решение неравенства x²+3a²+4ax≥2a+1 является решением неравенства x²+a²+(2x–1)a≥0

означает, что

{-a-sqrt(a) < -3a-1
{3a+1> -a+sqrt(a)

Решаем систему, получаем ответ....