Задача 46722 ...

polinanevolina

2020-04-11 18:15:24

Представьте двойной интеграл ∫∫_D f(x, y) dx dy в виде повторного интеграла, если область интегрирования D ограничена линиями x = y^2 и y = -1/2 x.

sova

2020-04-11 18:25:44

★

a) верно
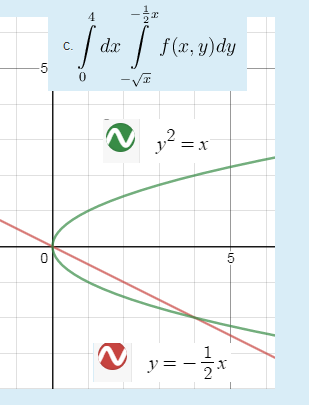
y=-(1/2)x ⇒ x=-2y
-2< y <0
y^2< x < -2y

и

с) верно.
x=y^2 ⇒ x= ± sqrt(y)

Верхняя ветвь : x=sqrt(y)
Нижняя ветвь : х=-sqrt(y)
0 < x < 4


Cм. рис.