Задача 46513 ...
Условие
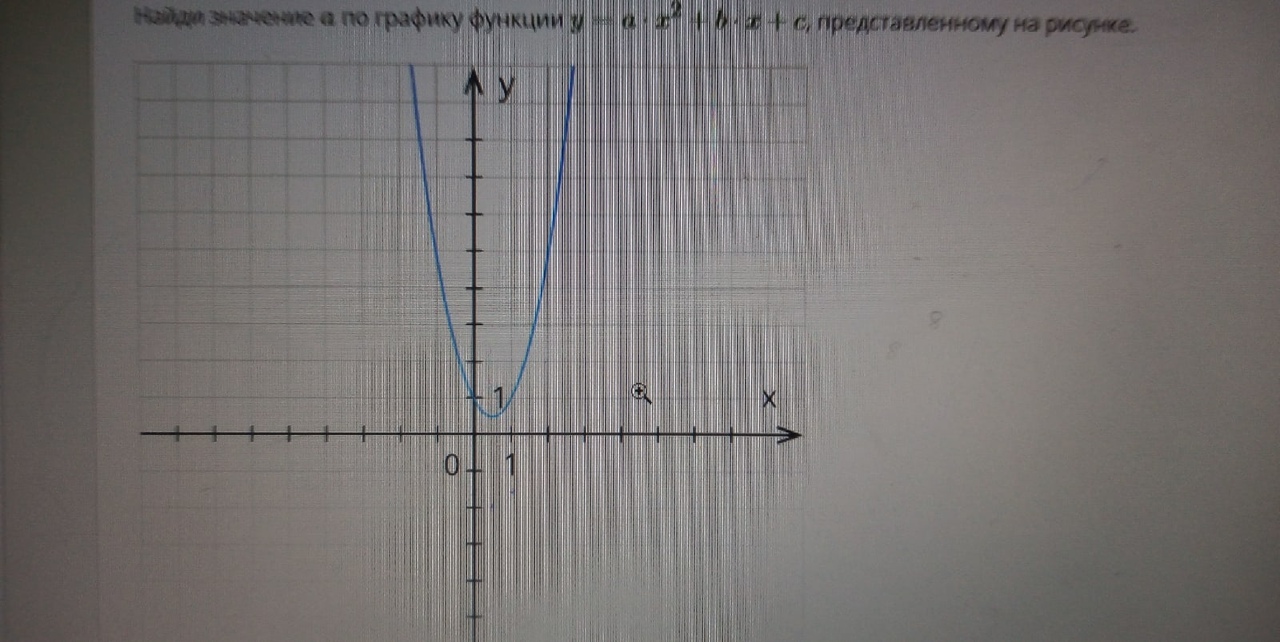
Решение
Значит с=1
у=ax^2+bx+1
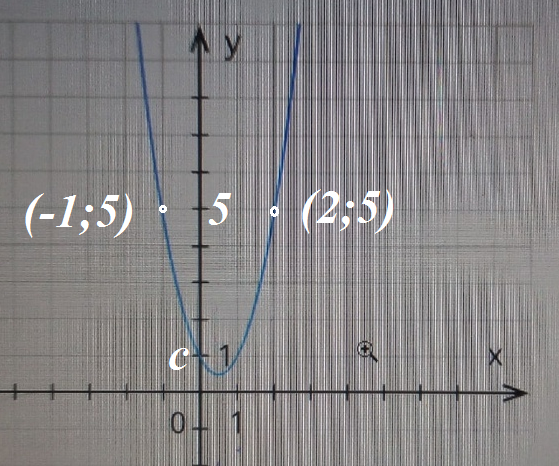
Две другие точки выбираем такие, чтобы у них были хорошие целочисленные координаты.
Это (2;5) и (-1;5)
Подставляем в уравнение и получаем систему:
{5=a*2^2+b*2+1
{5=a*(-1)^2-b+1
{4=4a+2b
{4=a-b
Умножаем второе на 2
{4=4a+2b
{8=2a-2b
Складываем
12=6a
[b]a=2[/b]
Все решения
то есть a*0^2 + b*0 + c = 1, то есть c=1.
из графика y(1) = 1, то есть a*1^2 + b*1 + 1 = 1, то есть
a+b+1 = 1,
a+b = 0,
из графика y(2) = 5, то есть
a*2^2 + b*2 + 1 = 5,
4a+2b + 1 = 5,
4a+2b = 4, теперь делим уравнение пополам:
2a+b = 2.
Теперь решаем систему двух уравнений:
a+b = 0
2a+b = 2,
вычтем из второго первое: (2a+b) - (a+b) = 2 - 0,
2a + b - a - b = 2,
a = 2.
Ответ. a = 2.
