Задача 46143 ...

slava191

2020-04-06 12:31:38

Пятиугольник ABCDE вписан в окружность единичного радиуса. Известно, что AB = sqrt(2), ∠ABE = π/4; ∠EBD = π/6; BC = CD

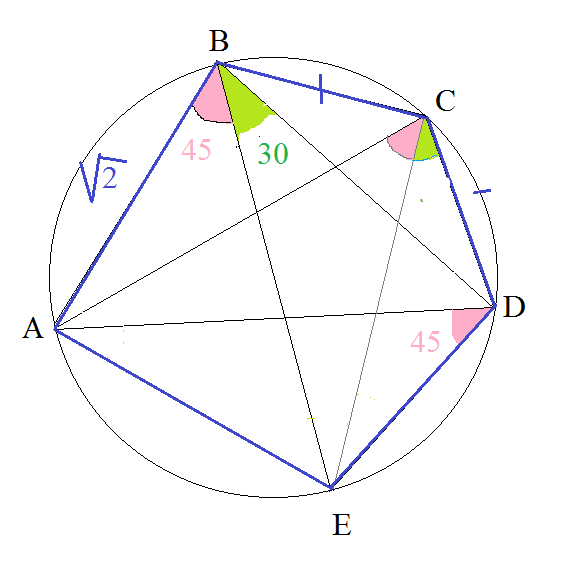
а) Докажите, что центр окружности лежит на одной из диагоналей пятиугольника

б) Найдите площадь пятиугольника [л16]

sova

2020-04-06 21:16:14

★

[red]a)[/red]
Δ ABD вписан в окружность.
По теореме синусов:

[m]\frac{AB}{sin\angle ADB}=2R[/m]

По условию
AB=sqrt(2)
R=1

Значит,
[m]sin\angle ADB=\frac {\sqrt{2}}{2}[/m] ⇒ [m]\angle ADB=45^{o}[/m]

[m]\angle ABE= \angle ADE=45^{o}[/m], как углы, опирающиеся на

одну и ту же дугу AE

∠ BDE= ∠ ADB+ ∠ ADE=45 ° +45 ° =90 °

BE-[i] диаметр окружности.[/i]

Центр окружности О лежит на диагонали BD пятиугольника

[red]б)[/red]

По теореме синусов для Δ BED

[m]\frac{ED}{sin30^{o}}=2[/m] ⇒ ED=1;

BE-[i] диаметр окружности.[/i] ⇒ ВЕ=2

По теореме Пифагора

[b]BD=sqrt(3)[/b]

⇒ sin ∠ BCD=sqrt(3)/2; ∠ BCD=120 °

BC=CD=[b]1[/b]

Четырехугольник ABDE вписан в окружность.

Сумма противолежащих углов равна 180 °

⇒ ∠ BAE + ∠ BDE=180 ° ⇒ ∠ BAE =90 °

Δ BAE - прямоугольный равнобедренный, АВ=АЕ=[b]sqrt(2)[/b]


S_(пятиугольника)=S_( Δ АВЕ)+S_( Δ BDE)+S_( Δ BCD)=

=[m]\frac{1}{2}AB\cdot AE +\frac{1}{2}BD\cdot DE + \frac{1}{2}1\cdot 1\cdot sin \angle BCD=[/m]

[m]=1+\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{4}=1+\frac{3\sqrt{3}}{4}[/m]

О т в е т. [m]1+\frac{3\sqrt{3}}{4}[/m]