Задача 46097 Помогите пожалуйста решить с подробным...
Условие
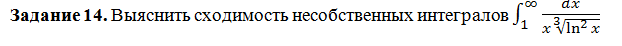
Решение
∫ ^( +∞ )_(1)dx/(x∛(ln^2x))=∫ ^( 2)_(1)dx/(x∛(ln^2x))+∫ ^( +∞ )_(2)dx/(x∛(ln^2x))
Первый несобственный интеграл второго рода.
Особенность в точке x=1
По определению:
∫ ^( 2)_(1)dx/(x∛(ln^2x))=lim_( ε → +0)∫ ^( 2)_(1- ε )dx/(x∛(ln^2x))=
=lim_( ε → +0)3∛(lnx)|^( 2)_(1- ε )=3*∛ln2 - 3*∛ln1=3*∛2-3*0=3∛2
Второй - несобственный интеграл первого рода
По определению:
∫ ^( +∞ )_(2)dx/(x∛(ln^2x))=lim_(A → + ∞ )∫ ^( A )_(2)dx/(x∛(ln^2x))=lim_(A → + ∞ )3∛(lnx)|^( A)_(2)=3*(lim_(A → + ∞ )∛ln(A))-3*∛(ln2)= [b]+ ∞[/b] -3∛(ln2)= +∞
Один сходится, второй расходится.
Сумма расходится....