Задача 46039 ...

marinichvika15

2020-04-05 18:36:40

2sin(-2x-pi/3) ≤ sqrt(3)

sova

2020-04-05 18:55:15

★

sin(-2x-(π/3) ≤ sqrt(3)/2

i]Замена переменной:[/i]
-2x - (π/3)=t

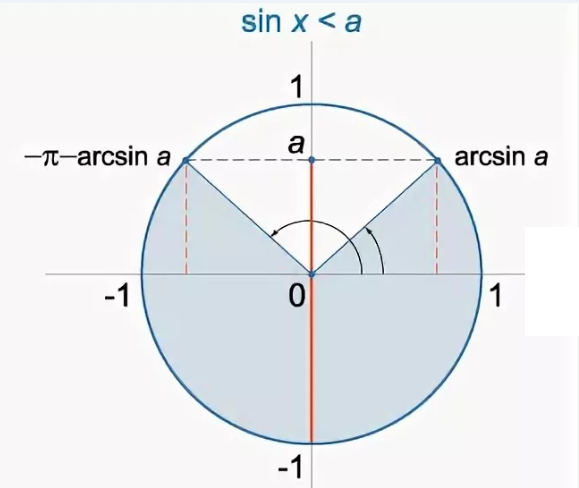
sint ≤ sqrt(3)/2 ⇒ cм. рис.

arcsin (sqrt(3))/2)=π/3



-π -(π/3)+2πn ≤ t ≤ (π/3)+2πn, n ∈ Z

-(4π/3)+2πn ≤ t ≤ (π/3)+2πn, n ∈ Z

Обратная замена:

-(4π/3)+2πn ≤ -2x - (π/3) ≤ (π/3)+2πn, n ∈ Z

Прибавляем (π/3)

-(4π/3)+(π/3)+2πn ≤ -2x ≤ (π/3)+(π/3)+2πn, n ∈ Z

-π+2πn ≤ -2x ≤ (2π/3) + 2πn, n ∈ Z

Делим на (-2), меняем знак:

(π/2)-πn ≥ x ≥ - (π/3) - πn, n ∈ Z

Пишем в привычном виде:

- (π/3) - πn ≤ х ≤ (π/2)-πn, n ∈ Z

обозначим

-n=k

[b]- (π/3) +πk ≤ х ≤ (π/2)+πk, k ∈ Z[/b]