Задача 46038 ...
Условие
математика 10-11 класс
572
Решение
★
(2π/3)-(π/2)+2πn ≤ -5x ≤ (4π/3)-(π/2)+2πn, n ∈ Z
(π/6)+2πn ≤ -5x ≤ (5π/6)+2πn, n ∈ Z
-(π/30)-(2π/5)*n ≥ x ≥ -(π/6)-(2π/5)*n, n ∈ Z
-(π/6)+(2π/5)*k ≤ x ≤ (-π/30) +(2π/5)*k, k ∈ Z, k=-n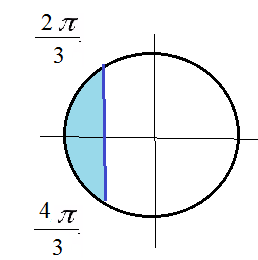
Все решения
По формуле приведения cos(pi/2-a)=sina получаем
sin(5x) ≤ -1/2.
-5pi/6+2pik ≤ 5x ≤ -pi/6+2pik.k ∈ z
-pi/6 +2pik/5 ≤ x ≤ -pi/30+2pik/5, k ∈ z
