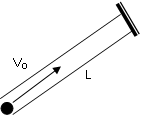
Шарик запустили вверх внутри трубки наклоненной под углом 30 к горизонту. Сверху трубка закрыта упругой стенкой. Через время ? шарик вернулся к точке старта. Его вновь запустили вверх, увеличив начальную скорость вдвое. Он опять вернулся к точке старта через время ?. Определите начальную скорость шарика в первом эксперименте, если длина трубки 7,5 м. Ускорение свободного падения g=10 м/c2. Трения нет.
