Задача 45995 Вычислите площадь фигуры ограниченной...
Условие
предмет не задан
2383
Решение
★
S= ∫ ^(1)_(0) x(y)dy= ∫ ^(1)_(0)(y^2+1)dy=((y^3/3)+y)|^(1)_(0)=(1/3)+1=4/3 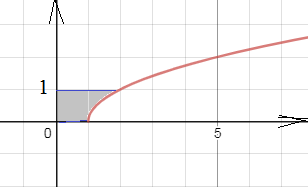
S= ∫ ^(1)_(0) x(y)dy= ∫ ^(1)_(0)(y^2+1)dy=((y^3/3)+y)|^(1)_(0)=(1/3)+1=4/3 