Задача 45891 ...
Условие
y = sqrt((x - 3)(x² - 7x + 12))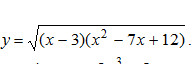
Решение
(x-3)(x^2-7x+12) ≥ 0
Раскладываем x^2-7x+12 на множители
по формуле:
[r]ax^2+bx+c=a(x-x_(1))(x-x_(2))[/r]
Находим дискриминант
D=(-7)^2-4*12=49-48=1
x_(1)=(7-1)/2=3; x_(2)=(7+1)/2=4
x^2-7x+12 =(x-3)(x-4)
Неравенство принимает вид:
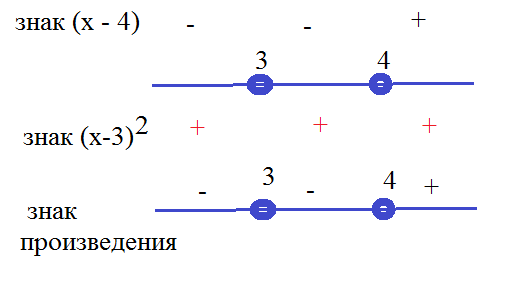
(x-3)(x-3)(x-4) ≥ 0
(x-3)^2*(x-4) ≥ 0
[red]Решаем методом интервалов[/red].
Находим нули функции. Это точки, в которых кривая пересекает ось Ох ( или касается!!!)
x=3 или x=4
и расставляем знаки:
_____ [3] ___ [4] ______
(см. рис.)
О т в е т. {3} U [4;+ ∞ )
Вывод. При переходе через точку х=3 знак не меняется.
Кривая касается оси Ох в точке х=3.
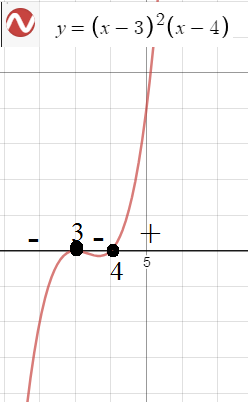
См. рис. 2 как она на самом деле выглядит
Расставляя знаки мы представляем себе именно расположение кривой.
Даже если еще не умеем ее строить.
Смотрите на графике
-,-,+
так же как на синей картинке
Особо хочу подчеркнуть, когда есть квадратный трехчлен,
например,
y=x^2-7x+12
Мы нашли его корни 3 и 4. График y=x^2-7x+12- парабола,
ветви вверх, значит знаки:
___+_ (3) __-__ (4) __+___
График квадратичной функции помогает быстро расставить знаки
Это полезно, если дана функция третьей степени, а ее[i] производная [/i]как раз[i] квадратичная функция[/i]
--------------------------------