Задача 45851 Помогите решить пожалуйста...
Условие
Решение
Все решения
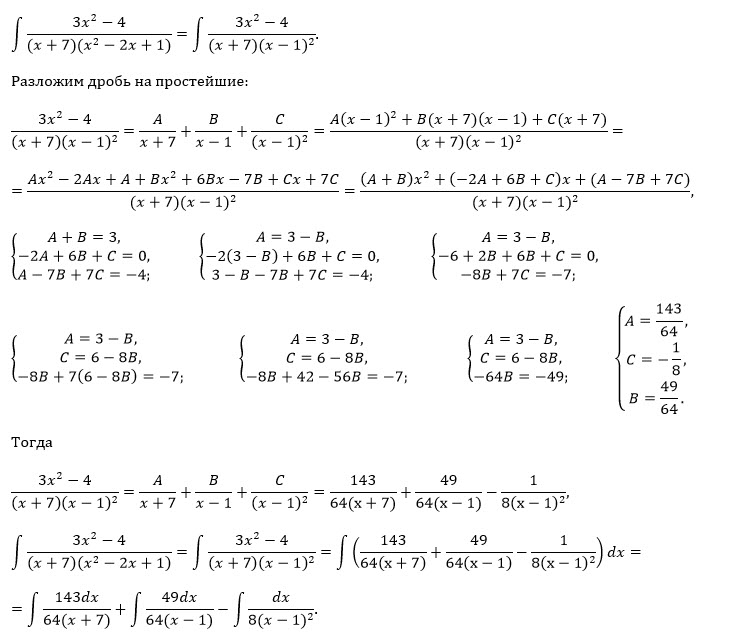
Правильную дробь разложим на простейшие дроби:
[m]\frac{3x^2-4}{(x+7)(x-1)^2}=\frac{A}{x+7}+\frac{B}{x-1}+\frac{D}{(x-1)^2}[/m]
Приводим правую часть к общему знаменателю и приравниваем числители:
3x^2-4=A*(x-1)^2+B*(x+7)*(x-1)+D*(x+7)
Применяем [b]метод частных значений[/b]
Выбираем такие значения, при которых выражения в скобках обращаются в нуль:
При x=1
3*(-1)^2-4=A*0+B*0+D*(1+7)
-1=8D ⇒ [m]D=-\frac{1}{8}[/m]
При х=-7
143=64А ⇒ [m]A=\frac{143}{64}[/m]
и любое третье значение, например,
при x=0
-4=A-7B+7D
7B=4+ [m]\frac{143}{64}[/m])+7* [m](-\frac{1}{8})[/m]
7B=[m]\frac{343}{64}[/m]
[m]В=\frac{49}{64}[/m]
[m]\int \frac{3x^2-4}{(x+7)(x^2-2x+1)}dx=
\int (\frac{A}{x+7}+\frac{B}{x-1}+\frac{D}{(x-1)^2})dx=[/m][m]=Aln|x+7|+Bln|x-1|-D\frac{1}{x-1}+C[/m]
где
[m]D=-\frac{1}{8}[/m]
[m]A=\frac{143}{64}[/m]
[m]В=\frac{49}{64}[/m]