Задача 45845 Помогите пожалуйста решить ...
Условие
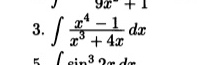
Решение
Выделяем целую часть.
Можно делить углом.
Можно "искусственно" выделить в числителе знаменатель:
x^4-1=x^4+4x^2-4x^2-1=(x^4+4x^2)-(4x^2+1)=x*(x^3+4x)-(4x^2+1)
И делим это выражение на знаменатель:
[m]\frac{x^4-1}{x^3+4x}=\frac{x\cdot(x^3+4x)}{x^3+4x}-\frac{4x^2+1}{x^3+4x}=x-\frac{4x^2+1}{x^3+4x}[/m]
Раскладываем правильную дробь [m]\frac{4x^2+1}{x^3+4x}[/m]
на простейшие [i]методом неопределенных коэффициентов.[/i]
Для этого знаменатель раскладываем на множители
x^3+4x=x*(x^2+4)
[m]\frac{4x^2+1}{x^3+4x}=\frac{A}{x}+ \frac{Mx+N}{x^2+4}[/m]
Коэффициенты А, M, N и есть неопределенные, их надо найти
из равенства дробей.
Приводим дроби справа к общему знаменателю:
[m]\frac{4x^2+1}{x^3+4x}=\frac{A\cdot (x^2+4)+x\cdot (Mx+N)}{x\cdot (x^2+4)}[/m]
Дроби равны, знаменатели равны, осталось приравнять числители:
[m]4x^2+1=A\cdot (x^2+4)+x\cdot (Mx+N)[/m]
[m]4x^2+1=Ax^2+4A+Mx^2+Nx[/m]
[m]4x^2+1=(A+M)x^2+4A+Nx[/m]
Два многочлена равны, если равны степени ( у нас оба квадратные)
и равны коэффициенты при одинаковых степенях перемнных:
при x^2
4=A+M
при х
0=N
при x^(0)
1=4A
A=1/4
M=4-(1/4)=15/4
[m]\int \frac{x^4-1}{x^3+4x}dx=\int xdx- \frac{1}{4}\int\frac{dx}{x}-\frac{15}{4}\int \frac {xdx}{x^2+4}=[/m] [m]\frac{x^2}{2}- \frac{1}{4}ln|x|-\frac{15}{8}ln|x^2+4|+C[/m]