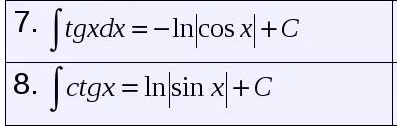Задача 45822 ...

gosha_

2 апреля 2020 г. в 13:40

1. Найти общий интеграл дифференциального уравнения
y'=tg⁡x∙tg⁡y
2. Найти общий интеграл дифференциального уравнения
3x⁴·y²·y'=y⁶–4x⁶
3. Найти общий интеграл дифференциального уравнения
xy'–y=8x³ ·cos²⁡x

sova

2 апреля 2020 г. в 15:26

1)
Уравнение с разделяющимися переменными.

y`=dy/dx

dy=tgx·tgydx

dy/tgy=tgx·dx

∫ ctgydy= ∫ tgxdx

Два табличных интеграла.

ln|siny|=–ln|cosx|+ln C ⇒ ln|siny|=lnC/|cosx| ⇒

siny=C/cosx

siny·cosx=C – общее решение

3.
Делим на x:
y`–(1/x)y=8x²·cos²x (#)

Линейное неоднородное первого порядка. Решают методом Бернулли (y=u(x)·v(x) )или методом вариации произвольной постоянной.

Решаем однородное:

y`–(1/x)y=0

Это уравнение с разделяющимися переменными

dy/y=dx/x


∫ dy/y= ∫ dx/x
ln|y|=ln|x|+ lnC

y=Cx

Метод вариации

y=C(x)·x

y`=C`(x)·x+C(x)

Подставляем в неоднородное (#) :

C`(x)·x+C(x)–(1/x)·C(x)·x=8x²·cos²x

C`(x)·x=8x²·cos²x

C`(x)=8x·cos²x

C(x)= ∫8x·cos²xdx

По частям
u=x ⇒ du=dx
dv=cos²xdx ⇒ v= ∫ cos²xdx= ∫ (1+cos2x)dx/2 =(1/2)x+(1/4)sin2x


C(x)=x·((1/2)x+(1/4)sin2x)– ∫ ((1/2)x+(1/4)sin2x)dx

C(x)=(1/2)x²+(1/4)x·sin2x–(1/4)x² –(1/8)·(–cos2x)+c

C(x)=(1/4)x²+(1/4)x·sin2x–(1/8)·(–cos2x)+c

y=C(x)·x

у=(1/4)x³+(1/4)x²·sin2x –(1/8)x·(–cos2x)+cx – о т в е т.