Задача 45746 Окружность касается сторон угла с...

slava191

2020-04-01 12:41:47

Окружность касается сторон угла с вершиной О в точках А и В. На этой окружности внутри треугольника АОВ взята точка С. Расстояния от точки С до прямых АО и ВО равны соответственно 8 и 18.

а) Докажите, что углы АВС и САО равны.

б) Найдите расстояние от точки С до прямой AB. [16п15]

sova

2020-04-01 14:39:15

★

Стороны угла - касательные к окружности.
По свойству касательных, проведенных к окружности из одной точки:
[b]АО=ОВ[/b]
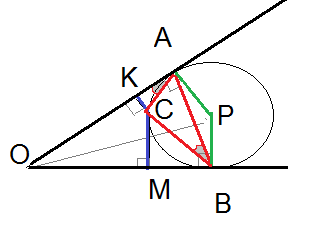
Обозначим центр окружности Р.
Так как касательная [i]перпендикулярна[/i] радиусу, проведенному в точку касания, то[b] РА ⊥ OA[/b] и [b]PB ⊥ OB[/b]
и
[b]ОР[/b]- [i]биссектриса[/i] угла О

∠ САО - угол между касательной и хордой, измеряется половиной дуги АС, заключенной между ними.
∠ АВС - вписанный угол, измеряется половиной дуги АВ, на которую он опирается.

[b]∠ САО=∠ АВС [/b]

б)
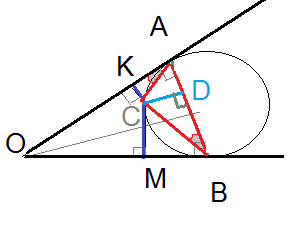
Проводим СD ⊥ AB
Δ АКС~ Δ CDB
ΔACD~ ΔOCM

CD=sqrt(CK*CM)=sqrt(8*18)=[b]12[/b]