Задача 45737 Помогите пожалуйста!!!!!!!!!! С...
Условие
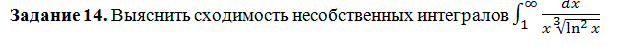
математика
764
Решение
★
Cчитаем по формуле
∫ u^(-2/3)du=u^(1/3)/(1/3)=3∛u
По определению:
∫ ^( +∞ )_(1)dx/(x∛(ln^2x))=lim_(A → + ∞ )∫ ^( A )_(1)dx/(x∛(ln^2x))=lim_(A → + ∞ )3∛(lnx)|^( A)_(1)=3*(lim_(A → + ∞ )∛ln(A))-3*∛(ln1)= [b]+ ∞[/b] -3*0= +∞
Но можно применять формулу Ньютона-Лейбница так же как в случае определенного интеграла, понимая, что подстановка + ∞ - это вычисление предела на + ∞ :
∫ ^( +∞ )_(1)dx/(x∛(ln^2x))=3∛lnx)|^( +∞)_(1)=3*(∛ln(+ ∞))-3*∛(ln1)= [b]+ ∞[/b] -3*0= +∞