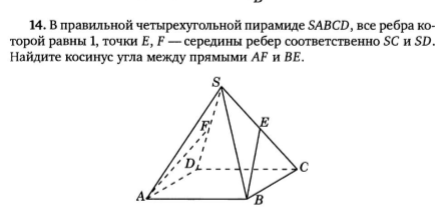
Задача 45655 В правильной четырехугольной пирамиде...

ann991

30 марта 2020 г. в 20:13

В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, F — середины ребер соответственно SC и SD. Найдите косинус угла между прямыми AF и BE.

sova

30 марта 2020 г. в 22:25

★

FE– средняя линия Δ SDC
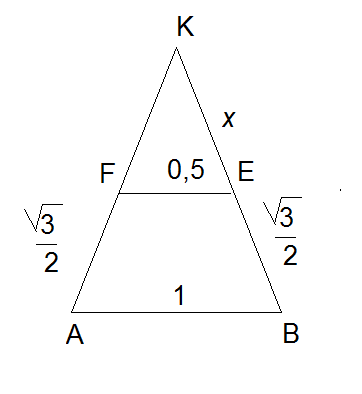
FE=0,5

BE=AF=√3/2 ( высоты равносторонних треугольников SBC и SDC cо стороной 1)

Продолжим стороны AF и DE до пересечения.
см. рис.

FE – средняя линия Δ АВК
AF=FK
AK=BK=√3

По теореме косинусов:
AB²=AF²+BF²–2AF·BF·cos φ

1=3+3–2·√3·√3·cos φ

cos φ =5/6