Задача 45629 а) Докажите, что высота, опущенная на...

slava191

30 марта 2020 г. в 13:20

а) Докажите, что высота, опущенная на гипотенузу прямоугольного треугольника, делит треугольник на два подобных треугольника.

б) Найдите высоту прямоугольного треугольника, опущенную на гипотенузу, если известно, что основание этой высоты делит гипотенузу на отрезки, равные 1 и 4. [16п10]

sova

30 марта 2020 г. в 14:32

★

a) Δ АВС – прямоугольный ( ∠ С=90 ° )

Сумма острых углов прямоугольного треугольника равна 90 °

Тогда
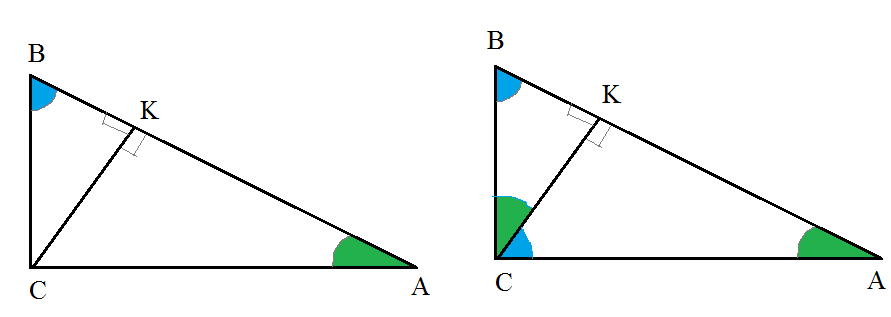
∠ ВСК= ∠ВАС ( выделены зелёным цветом на рис. 2)
∠ АВС= ∠ АСК ( выделены синим цветом на рис.2)

Δ ВСК ~ Δ АСК по двум углам

Из подобия:

[m]\frac{BK}{CK}=\frac{CK}{AK}[/m]

[m]CK^2=BK\cdot AK[/m]

[m]СK=\sqrt{BK\cdot AK}[/m] – высота прямоугольного треугольника проведенная из вершины прямого угла на гипотенузу есть среднее геометрическое между отрезками гипотенузы, на которые основание высоты делит гипотенузу

б)
BK=1; AK=4

[m]СК=\sqrt{1\cdot 4}[/m]=2

О т в е т. б) 2