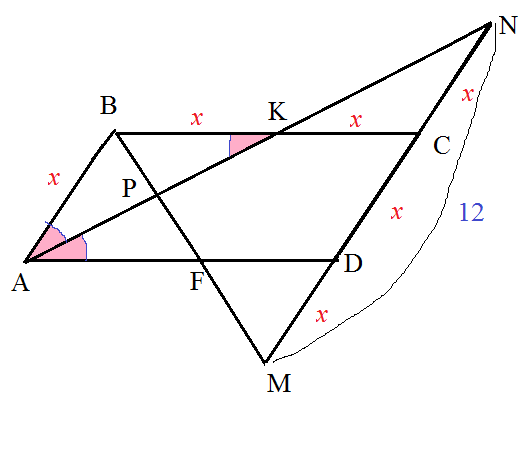
Задача 45627 Сторона ВС параллелограмма ABCD вдвое...

slava191

2020-03-30 13:15:27

Сторона ВС параллелограмма ABCD вдвое больше стороны АВ. Биссектрисы углов А и В пересекают прямую CD в точках M и N.

а) Докажите, что MD = CN.
б) Найдите стороны параллелограмма, если MN = 12. [16п8]

sova

2020-03-30 15:07:06

★

О т в е т. 4 и 8
Решение.

Пусть АВ=[b]х[/b]; тогда BC=[b]2x[/b]

Δ АBF - равнобедренный
∠ BAK= ∠ KAD - так как АК - биссектриса
∠BKP= ∠ KAD - [i]внутренние накрест лежащие[/i] при параллельных ВС и AD и секущей AK

По свойству транзитивности:
[b]∠BKP= ∠ BAK[/b]

Тогда ВК=х; KC=x

∠ АВС= ∠ КСN -[i] внутренние накрест лежащие[/i] при параллельных AB и CD и секущей BC
∠ ВКA= ∠ NKC как [i]вертикальные[/i]
Δ АВK= Δ KCN по стороне и двум прилежащим к ней углам.

⇒ AB=BC=KC=CN=x

∠ ВAF= ∠ FDM -[i] внутренние накрест лежащие[/i] при параллельных AB и CD и секущей AD
∠ ВFA= ∠ DFM как [i]вертикальные[/i]
Δ AВF= Δ FDM по стороне (AF=FD=x) и двум прилежащим к ней углам.

⇒ AB=AF=FD=DM=x

MN=MD+DC+CN=x+x+x

По условию MN = 12

x+x+x=12

3x=12

[b]x=4
[/b]

2х=2*4=8

О т в е т. 4 и 8