Задача 45625 Вне прямоугольного треугольника АВС на...

slava191

30 марта 2020 г. в 13:10

Вне прямоугольного треугольника АВС на его катетах АС и ВС построены квадраты ACDE и BCFG. Продолжение медианы СМ треугольника АВС пересекает прямую DF в точке N.

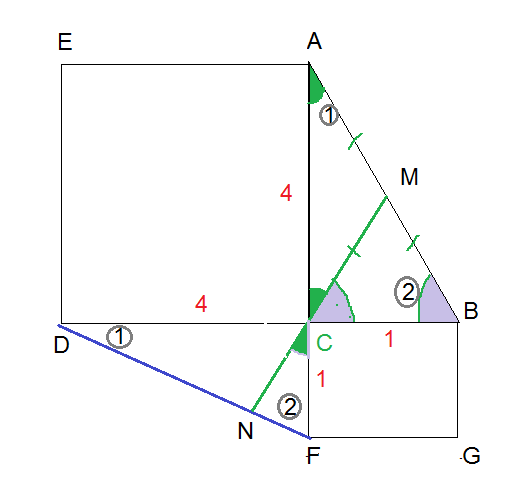
а) Докажите, что CN является высотой треугольника CDF.

б) Найдите отрезок CN, если AC = 1, BC = 4. [16п6]

sova

30 марта 2020 г. в 20:23

★

В Δ АВС: АС– катет и ВС – катет ⇒ ∠ С=90 ° или ∠АСB=90 °

ACDE– квадрат ⇒ ∠ ACD=90 ° и АС=DC
BCFG– квадрат ⇒ ∠ BCF=90 ° и BС=CF

∠ АCB=90 °

Значит ∠ FCD=90 °

Прямоугольные треугольники СDF и ABC равны по двум катетам.
АС=DC =4
BС=CF=1

Значит и соответствующие углы в этих треугольниках равны
∠ BAC= ∠ CDF= ∠ 1 ( расположены против сторон ВС и СF)
∠ ABC= ∠ DFC= ∠ 2 ( расположены против сторон AD и DC)

∠ВАС= ∠ MСA= ∠ 1, так как медиана СМ прямоугольного треугольника равна половине гипотенузы и Δ АМС – равнобедренный
Аналогично
∠МВС= ∠ МСВ= ∠ 2.

∠ FCN=∠ МCA= ∠ 1 как вертикальные

Значит ∠ FCN+ ∠ CFN= ∠ 1+ ∠ 2 = 90 ° ⇒ ∠ СNF=90 °

и СN ⊥ DF

По теореме Пифагора:
DF²=DС²+СF²=1²+4²=17

Так как

S _ΔDFC=(1/2)DF·CN и S (ΔDFC)=(1/2)DC·CF, то

DF·CN=DC·CF

СN=1·4/√17=4√17/17


О т в е т. 4√17/17