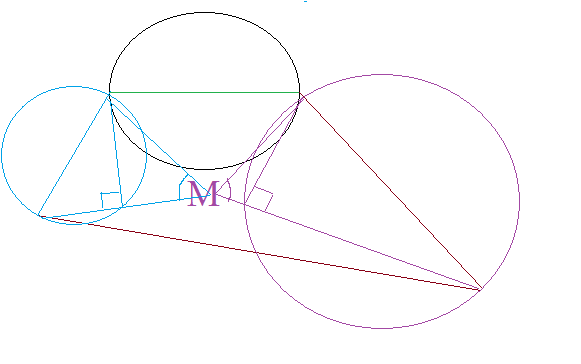
Задача 45622 Четыре окружности, построенные как на...
Условие
а) Докажите, что диагонали четырёхугольника ABCD перпендикулярны.
б) Найдите площадь четырёхугольника ABCD, если длина диагонали АС равна sqrt(2), а отрезки, соединяющие середины противоположных сторон, перпендикулярны. [16п4]
Решение
Если внутри четырехугольника есть точка М, не принадлежащая всем четырем окружностям, то из этой точки все стороны четырехугольника видны по острым углом.
∠ 1 <90 °
∠ 2 <90 °
∠ 3 <90 °
∠ 4 ∠ 90 °
Но тогда 360 °[b] =[/b] ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4[b] < 360 ° [/b]
Что невозможно. Значит
M- точка, в которой пересекаются все четыре окружности
и
∠ 1= ∠ 2= ∠ 3= ∠ 4=90 ° ⇒ диагонали четырехугольника [i]взаимно перпендикулярны.[/i]
б)
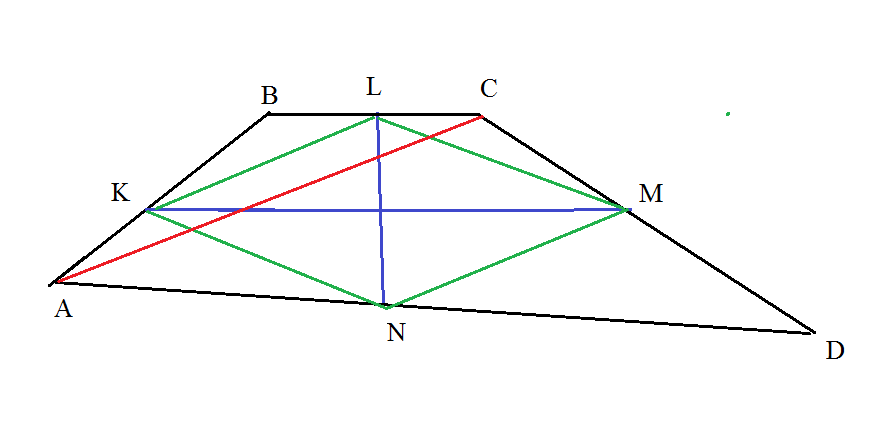
На рис. 2
К-середина АВ
L-середина ВС
M- середина CD
N- середина AD
Тогда
KL=MN ( KL - средняя линия Δ АВС, MN - средняя линия Δ АDС)
KN=LM (KN-средняя линия Δ АВD, MN - средняя линия Δ BCD)
⇒ KLMN - параллелограмм, диагонали которого взаимно перпедикулярны.
Значит KLMN- ромб
KL || AC
KN|| BD
AC ⊥ BD ⇒ KLMN - квадрат ⇒ BD=AC
S_(ABCD)=(1/2)AC*BD=(1/2)*sqrt(2)*sqrt(2)=1
О т в е т. 1